ResNet
마이크로소프트 팀이 개발한 ResNet은 잔차(Residual) 라는 개념을 도입하였고, 그 결과 ILSVRC 2015에서 1위를 차지하였다.
Abstract
- 딥러닝에서 신경망(Neural Network)이 깊을수록 Train은 더 어려워집니다. (오버 피팅이 발생할 확률이 높다.)
- 그래서 ResNet 에서는 깊은 신경망에서도 training을 용이하게 하기 위한 residual learning framework(잔차 학습) 를 제시합니다.
- 함수를 새로 만드는 방법 대신 residual function(잔차 함수)을 train에 사용하는 것으로 Layer를 재구성 합니다.
- ResNet의 residual 네트워크는 optimize를 더 쉽게 하고, 더 깊은 모델에서도 상당한 accuracy를 얻는 것을 empirical evidence showing(경험적으로 보여줍니다).
- 결과적으로 152개의 Layer를 쌓아 기존의 VGG Net 보다 좋은 성능을 내면서 복잡성을 주였고, ILSVRC 2015에서 1등을 하였습니다.
Introduction
- Deep Convolutional Neural Networks 는 이미지 분류 분야에서 중요한 돌파구가 되었습니다.
- 최근 자료들을 통해 네트워크의 깊이가 중요한 요소이며 ImageNet에서 깊은 모델들이 좋은 결과를 낸다는 것을 보여주고 있습니다.
- 이 논문의 저자는 “과연 더 많은 Layer를 쌓는 것만큼 Network의 성능은 좋아질까 ?” 라는 의문을 가졌습니다. 왜냐하면 이와 관련해서 악명 높은 많은 문제 problem of vanishing / exploding gradients 가 발생하기 때문입니다. 이러한 문제는 SGD 와 backpropagation를 적용한 첫 10개의 Layer에서는 normalized initialization, intermediate normalization Layers 를 통해 대부분 해소 되었습니다.
- 하지만 네트워크 깊이가 증가할수록, accuracy가 감소되는 degradation 이 발생한다.
- \(\rightarrow\) 네트워크의 깊이가 깊어짐에 따라 정확도가 포화하고, 급속하게 감소하는 것
- \(\rightarrow\) Overfitting과 다르게 단지 더 많은 Layer들이 추가 되어서이기 때문인데 이러한 근거는 train error, test error 둘 다 높다는 것을 보고 확인할 수 있습니다.
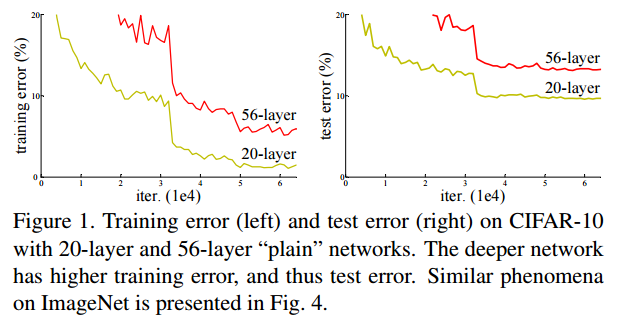
- 이 문제는 모든 시스템들이 optimize 하기 쉽지 않다는 것을 보여주기 때문에 얕은 구조와 더 깊은 아키텍처를 비교해 보여주려고 합니다.
- Identity mapping layer 를 추가해봤지만 실험을 통해 좋은 solution이 아니라는 결과를 얻었습니다.
- 그래서 ResNet 에서는 Deep residual learning framework 라는 개념을 도입하여 degradation 문제를 해결하려고 합니다.
- 추가된 Layer가 identity mapping이고, 추가되지 않은 다른 레이어들은 더 얕은 모델에서 학습된 Layer를 사용하는 것
- \(\rightarrow\) 쌓여진 Layer가 desired underlying mapping에 바로 적용되는 것이 아니라 residual mapping에 적용하도록 한다.
기존의 네트워크는 입력 \(x\)를 받고 Layer를 거쳐 타겟값 \(y\)로 mapping 하는 함수 \(H(x)\)를 얻는 것이 목적이면, Residual Learning은 출력과 입력의 차인 \(H(x)-x\)를 얻도록 목표를 수정하는 것입니다. 이는 nonlinear layer(비선형 적인) mapping \(F(x)=H(x)-x\)를 최소화시켜야 하고 이는 출력과 입력의 차이를 줄인다는 의미가 됩니다.
여기서 입력 \(x\)의 값은 변경할 수 없으므로 \(F(x)\)가 0이 되는 것이 최적의 해이고, 결국 \(H(x)=x\)가 되는 \(H(x)\)를 \(x\)로 mapping 하는 것이 학습의 목표가 됩니다.
이를 전개하면 \(H(x)=F(x)+x\)의 형태가 됩니다. \(\rightarrow\) residual mapping이 기존 mapping 보다 optimize 하기 쉽다는 것을 가정합니다. 그러한 이유는 이전에는 Unreferenced mapping인 알지 못하는 최적의 값으로 \(H(x)\)를 근사하도록 학습시켜야 한다는 점 때문에 어려움이 있었는데, \(H(x)=x\) 라는 최적의 목표값이 사전에 제공되기 떄문에 Identity mapping인 \(F(x)\)가 학습이 더 쉬워지기 때문입니다.
결과적으로 \(H(x)=F(x)+x\)는 Shortcut Connection과 동일한데 이는 하나 또는 하나 이상의 Layer를 Skip 가능하게 만들어 줍니다. \(\rightarrow\) 단순히 입력에서 출력으로 바로 연결되는 shortcut만 추가하면 되기 떄문이다.
ResNet에서는 Shortcut Connection을 위해 identity mapping을 수행하고, 그 결과는 stacked layer의 output에 더해집니다.
ResNet에서는 출력과 입력 간의 차에 대해 학습을 시키면 해결 할 수 있다고 생각하였습니다.
\(\rightarrow\) 입력 \(x\)값을 출력 \(F(x)\)에 더하는 identity mapping (Shortcut Connections)
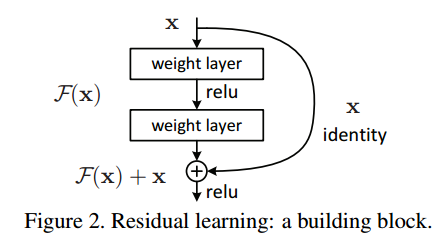
\(F(x) = W_2 \times ReLU(W_2 \times x)\)
만약 \(F(x)\)와 \(x\)가 차원이 다를 경우, \(W_s\) projection matrix를 곱하여 차원을 같게 만든 후 더함.
\(\rightarrow\) \(y = F(x) + W_s \times x\)
이 Identity Shortcut Connection 은 추가적인 parameter도 필요하지 않고 복잡한 곱셈 연산도 필요하지 않는 것이 장점입니다. \(\rightarrow\) 곱셈 연산에서 덧셈 연산으로 변형되어 몇 개의 Layer를 건너뛰는 효과를 가지고 있습니다.
이를 이용한 네트워크는 backpropagation, SGD 로 end-to-end 학습이 가능하며, solver 수정없이 common library 를 이용하여 쉽게 구현이 가능하다.
ResNet은 실험적인 방법을 통해 degradation 문제를 보이고 논문의 방법을 평가합니다.
\(\rightarrow\) PlainNet과 달리 ResNet이 optimize 하기 더 쉽다.
\(\rightarrow\) ResNet은 Depth가 증가해도 더 쉽게 accuracy를 얻을 수 있다.
Related Work
- Residual Representations
- Shortcut Connections
\(\rightarrow\) ResNet 에서 사용한 Identity shortcut 기법의 장점인 parameter 필요 X & 복잡한 곱셈 연산 필요 X 등을 언급하였다.
Deep Residual Learning
Residual Learning
\(H(x)\) : original mapping, \(F(x)\) : residual mapping, \(F(x)+x\) : original function
앞서 Introduction에서 설명한 것을 다시 얘기합니다.
만약 residual learning의 재구성을 통해, residual mapping이 optimal(최적) 인 경우 solver는 단순히 residual mapping에 접근하기 위해 multi nonlinear layers의 weight 를 얻기가 더 쉬울 것입니다.
\(\rightarrow\) 실제로는 Identity mapping이 최적일 가능성이 낮다고 합니다. 하지만 ResNet에서 제안하는 재구성 방식은 문제에 preconditioning을 추가하는데 도움을 줍니다 따라서 preconditioning으로 인해 optimal function이 zero mapping보다 identity mapping에 더 가깝다면, solver가 identity mapping을 참조하여 작은 변화를 학습하는 것이 새로운 function을 학습하는 것보다 더 쉬울 것이라고 본 논문에서 주장한다.
정리하자면, 재구성한 식 \(F(x)+x\)는 identity mapping이 optimal 일 경우를 가정하여 구성한 것으로 보인다. 그러나, 이는 가정일 뿐 실제로 depth가 깊어질수록 성능의 향상을 기대하는 경우엔 \(H(x)\)의 optimal이 identity라고 보기 어렵다.
그럼에도 \(F(x)+x\) 라는 식에서는 입력 x가 학습 시에 일종의 guide 로써 적용하여 학습을 도와주므로, identity가 optimal이 아닌 경우라도 이 재정의 은 여전히 긍정적인 효과를 기대할 수 있을 것이다. [참고]
Identity Mapping by Shortcut
ResNet에서는 모든 stacked layers 에 residual learning 을 적용한다. 다음 그림의 building block 을 다음과 같이 정의한다.
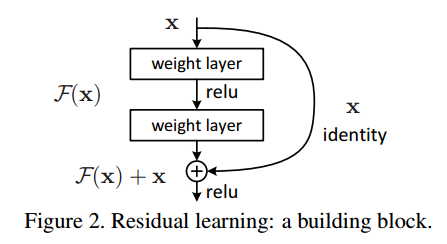
[Enq. 1] \(y=F(x, \{W_i\})+x\)
\(\rightarrow\) \(F(x, \{W_i\})\) : 학습 될 residual mapping (\(x\) : input, \(y\) : output)
\(\rightarrow\) 위 그림과 같이 Layer가 2개인 경우 \(F=W_2 \sigma(W_1 \times x)\)로 나타낼 수 있다. (\(\sigma\) : ReLU, \(bias\) : 생략)
\(\rightarrow\) \(F+x\) 연산은 shorcut connection, element-wise addition으로 수행되며, addition 후 second nonlinearity로 ReLU를 적용한다.
\(\rightarrow\) parameter도 없고 계산 복잡도도 없다.
\(\rightarrow\) 위 수식에서는 \(x\)와 \(F\)의 차원이 같을 것
[Enq. 2] \(y=F(x, \{W_i\}) + W_s \times x\)
\(\rightarrow\) [Enq. 1] 에서 \(F + x\) 연산은 2개의 차원이 같아야 한다. 동일하지 않다면 이를 위해 linear projection \(W_s\)를 적용할 수 있다.
\(\rightarrow\) [Enq. 1] 에서 square matrix로 \(W_s\)를 수용할 수 있지만, 성능 문제를 해결하기 위해 identity mapping 만으로도 충분하고 경제적이므로 \(W_s\)는 dimention matching 용도로만 사용한다.
[추가]
위 식을 conv Layer 상에서도 마찬가지로 identity mapping을 구현할 수 있다.
이 경우에는 dimension matching을 위해 \(1\times 1\) filter의 conv Layer를 이용하며, element-wise addition은 feature map 간의 channel-by-channel addition으로 수행된다.
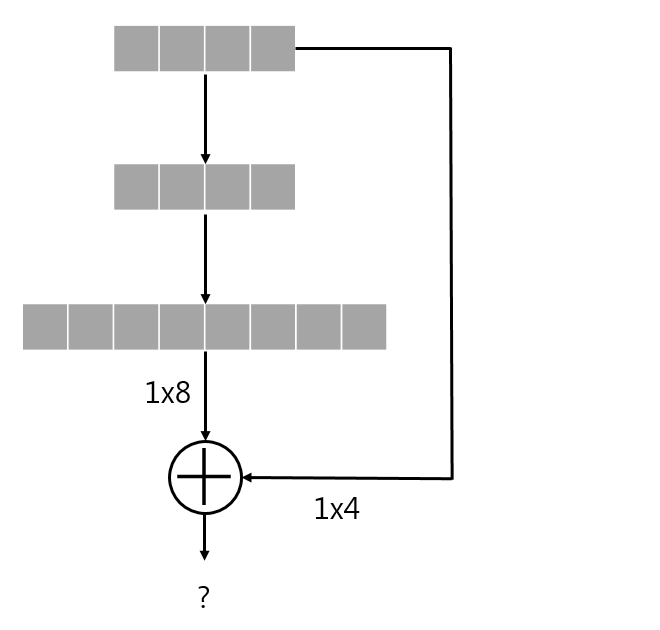
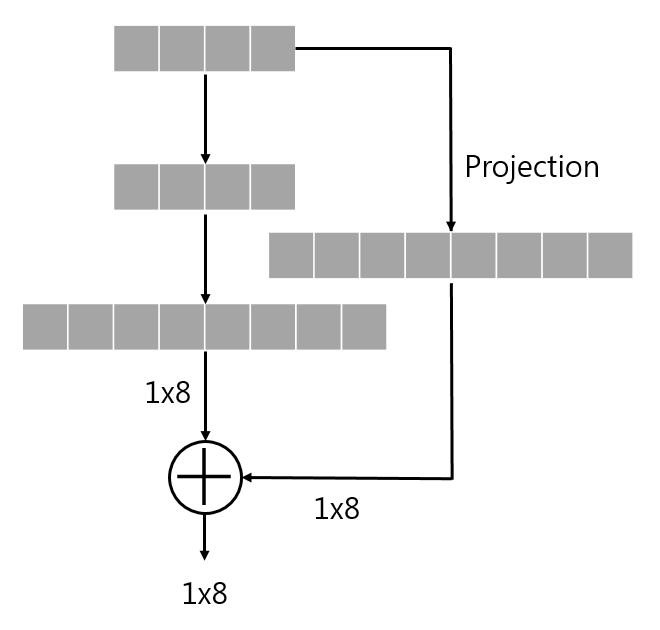
Network Architectures
ResNet 에서는 다양한 형태의 plain/residual network에 대해 테스트 했으며, 일관된 현상을 관찰하였습니다.
테스트에서 사용할 ImageNet dataset을 위한 두 모델은 다음과 같이 정의합니다.
plain network
- baseline은 주로 VGGNet 에 영감을 얻어 만들어 졌으며 conv layer는 대게 \(3\times 3\) filter를 가지며
- 동일한 output feature map size에 대해, layer는 동일한 수의 filter를 갖는다.
- feature map size가 절반이 될 경우, layer당 time complexity를 보전하기 위해 filter의 수를 2배로 한다.
- conv layer는 stride 2로 downsampling(Pooling) 하며, network는 global average pooling layer와 softmax를 사용한 1000-way FC layer로 끝난다.
- plain network는 VGG-19 에 비해 적은 수의 filter와 낮은 complexity를 가진다.
residual network
- plain network 기반으로 shortcut connection을 삽입하여 residual version의 network를 만든다.
- identity shortcut [Eqn. 1]은 input과 output이 동일한 dimension인 경우(실선) 직접 사용될 수 있으며, dimension이 증가하는 경우(점선) 아래 두 옵션을 고려한다.
- zero padding을 추가로 하여 dimension matching 후 identity mapping 수행
- [Eqn. 2]의 projection shortcut을 dimention matching에 사용
- shortcut connection이 다른 크기의 feature map 간에 mapping 될 경우, 두 옵션 모두 stride 2로 수행. (feature map의 크기가 달라지는 경우는 stride가 2인 con layer를 통한 downsampling을 거쳤기 떄문)

Implementation
논문에서 ImageNet dataset에 대한 실험은 AlexNet과 VGG의 방법을 따른다.
이미지는 scale augmentation를 위해 [256,480]에서 무작위하게 샘플링 된 shorter side를 사용하여 rescaling 된다.
\(244\times 244\) crop 은 horizontal flip with per-pixel mean subtracted 이미지 중에 무작위로 샘플링 되며, standard color augmentation도 사용된다.
- 각각의 conv layer와 activation 사이에는 batch normalization을 사용하며, He initialization 기법으로 weigth를 초기화하여 모든 plain/residual network을 학습한다.
- batch normalization에 근거해 dropout을 사용하지 않는다.
- learning rate는 0.1 에서 시작하여 error가 안정된 상태가 되면 learning rate를 10으로 나누어 적용하며, decay는 0.0001, momentum은 0.9로 한 SGD를 사용하였다.
- mini-batch size 는 256로 했으면, iteration은 총 600K회 수행된다.
Experiments
ImageNet Classification
ResNet 에서는 1000개의 class로 구성 된 ImageNet 2012 classification dataset에서 제안하는 방법을 평가했습니다.
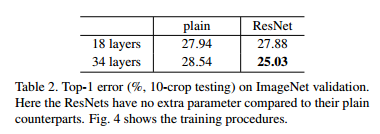

Plain Networks
먼저 18-Layer 및 34-Layer plain network를 평가합니다.
그 결과 plain에서는 18-Layer network에 비해, 34-Layer network의 validation error가 높은 것으로 보입니다.
34-layer plain network의 error가 학습 과정 전반에 걸쳐서 더 높게 나타나는 성능 저하 문제를 확인할 수 있습니다.
논문의 저자들은 여기서 직면하는 optimization difficulty가 vanishing gradients에 의한 것 같지는 않다고 주장합니다.
그 이유는 plain network가 batch normalizaion을 포함하여 학습했기 때문에 forward propagated signal의 분산이 0이 아니도록 보장했으며, backward propagation gradients가 healty norm을 보이는 것도 확인했기 때문입니다. 따라서 gradient vanishing 문제는 발생하지 않았다고 볼 수 있습니다.
다음 결과에 따르면 34-layer plain network가 여전히 경쟁력 있는 정확도를 달성했으며, 이는 solver의 작동이 이루어지긴 한다는 것을 의미한다. 그래서 저자들은 deep plain network는 exponentially low convergence rate를 가지며, 이것이 training error의 감소에 영향을 끼쳤을 거라 추측한다.
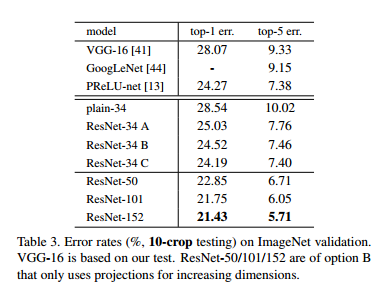
Residual Networks
다음으로 18-Layer 및 34-Layer residual network(ResNet)을 평가한다.
baseline architecture은 plain network와 동일하며, 각 \(3 \times 3\) filter pair에 shortcut connection을 추가했다. 모든 shortcut connection은 identity mapping을 사용하며, dimension matching을 위해서는 zero-padding을 사용한다. 따라서 대응되는 plain network에 비해 추가되는 parameter가 없다.
[Table. 2]와 결과 그림에서 알 수 있는 3가지 주요 관찰 결과는 다음과 같다.
- residual learning으로 인해 상황이 바뀌었다. 34-layer ResNet이 18-layer ResNet 보다 우수한 성능을 보인다. 또한, 34-layer ResNet이 상당히 낮은 training error를 보였으며, 이에 따라 상향된 validation 성능이 관측됐다. 이는 성능 저하 문제가 잘 해결됐다는 것과, 증가된 depth에서도 합리적인 accuracy를 얻을 수 있다는 것을 나타낸다.
- 34-layer ResNet은 이에 대응하는 plain network와 비교할 때, validation data에 대한 top-1 error를 3.5% 줄였다.
- 18-layer plain과 residual network 간에는 유사한 성능을 보였지만, 결과 그림에서 보듯 18-layer ResNet은 더욱 빠르게 수렴한다. 이는 network가 not overly deep 한 경우 plain network에서도 좋은 solution을 찾을 수 있다는 것으로 볼 수 있다.
Identity vs Projection Shortcut
위 [Table. 3] 에서는 다음 3가지 옵션에 대한 결과를 보여준다.
(A) zero-padding shortcut는 dimension matching에 사용되며, 모든 shortcut은 parameter-free로 한 경우
(B) projection shortcut는 차원을 늘릴 때만 사용되며, 다른 shortcut은 모두 identity로 한 경우
(C) 모든 shortcut을 projection으로 한 경우
3가지 옵션들은 모두 plain network보다 훨씬 나은 결과를 보여준다. 성능은 C > B > A 순서로 좋았다.
A 의 zero-padding 과정에 residual learning이 없어서 B 가 더 나은 성능을 보이고
C의 추가 parameter 가 많은 projection shortcut에 의해 B 보다 더 나은 성능을 보인다.
여기서 3가지 옵션 간의 차이는 미미한 것으로 보아 projection shortcut이 degradation problem을 해결하는데 필수적이지 않다는 것을 알 수 있다. 그래서 이 뒤부터는 메모리, 시간, 복잡성, 모델 크기 감소를 위해 옵션 (C)를 사용하지 않는다.
Identity shortcut은 아래에서 설명될 bottleneck architectures의 복잡성을 증가시키지 않는 점에서 특히 중요하다.
Deeper Bottleneck Architectures.
감당할 수 없는 training time에 대한 우려로 인해, buliding block을 bottleneck design으로 수정한다.
다음 그림처럼 각 residual function F, 2-layer stack 대신 3-layer stack을 사용한다.
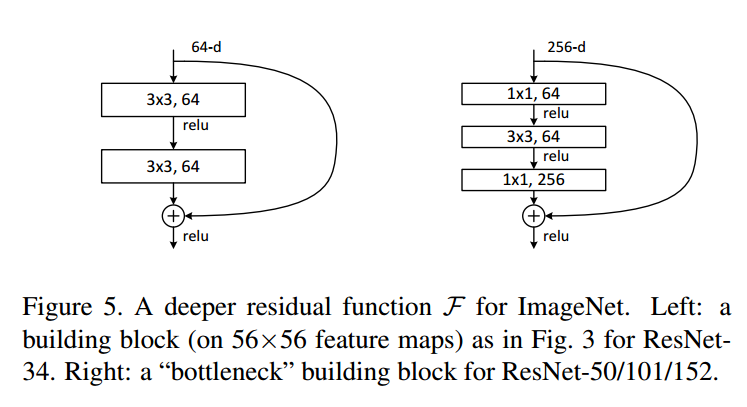
3개의 layer는 각각 순서대로 \(1\times 1, 3\times3, 1\times1\) conv layer 이며, \(1\times1\) conv layer는 dimension을 줄이거나 늘리는 용도로 사용하며, \(3\times3\) layer의 input/output의 dimension을 줄인 bottlenet으로 둔다.
여기서 parameter free인 identity shortcut은 이 architecture에서 특히 중요하다. 만약 위 그림의 오른쪽 다이어그램에서 identity shortcut이 projection으로 대체된다면, shortcut이 두 개의 high-dimensional 출력과 연결되므로 time complexity와 model size가 두 배 늘어난다. 따라서 identity shortcut은 이 bottleneck design을 보다 효율적인 모델로 만들어 준다.
50-Layer ResNet
34-layer ResNet의 2-layer block 들을 3-layer bottleneck block으로 대체하여 50-layer ResNet을 구성하였다. dimention matching을 위해 위의 옵션 (B)를 사용하였다.
\(\rightarrow\) (B) projection shortcut은 dimension을 늘릴 때만 사용되며, 다른 shortcut은 모두 identity다.
101-Layer and 152-Layer ResNet
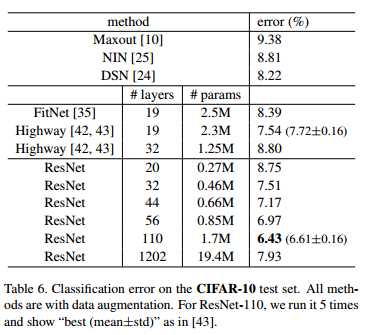
여기에 3-layer bottleneck block을 추가하여 101-layer 및 152-layer ResNet을 구성했다. depth가 상당히 증가했음에도 상당히 높은 정확도가 결과로 나왔다.
Comparison with State-of-the-art Methods

6가지 모델을 앙상블 기법을 적용하여 실험 결과 ResNet이 3.57% top-5 error를 달성하며, ILSVRC 2015에서 1등을 하였다.
CIFAR-10 and Analysis
CIFAR-10 dataset을 대상으로 모델 학습 및 검증 결과를 다룬다.
Analysis of Layer Responses.
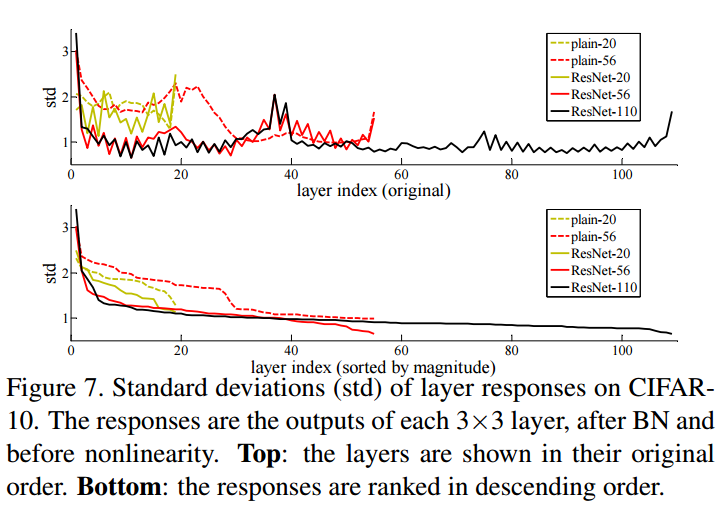
Plain/Residual Network의 각 layer responses의 표준편차를 보여준다. ResNet의 response가 plain network보다 적은걸 볼 수 있는데, 이는 residual function이 non-residual function보다 일반적으로 0에 가까울 것이라는 저자들의 basic motivation을 뒷바침한다.
Exploring Over 1000 Layers
1202-layer network는 110-layer network와 비슷한 training error를 보이지만 test는 좋지 못하였는데 overfitting이 발생한 것 같다고 말한다.
참조 사이트
https://sike6054.github.io/blog/paper/first-post/
(ResNet) Deep residual learning for image recognition 번역 및 추가 설명과 Keras 구현
Paper Information
sike6054.github.io
[논문 리뷰] Deep Residual Learning for Image Recognition - ResNet(1)
ResNet ResNet 이라는 이름으로 더 유명한 논문을 리뷰해보겠습니다. 최고의 빅데이터 분석 동아리 '투빅스' 과제 겸사겸사 하는 리뷰입니다. (사실 이게 아니라 구현 과제를 해야되는데 어렵네요...
jxnjxn.tistory.com
https://wandukong.tistory.com/18
[논문 리뷰] ResNet 논문 리뷰
오늘은 최근에 읽은 유명한 논문, ResNet을 리뷰해보려고 합니다. 논문 링크 : https://arxiv.org/abs/1512.03385 Deep Residual Learning for Image Recognition Deeper neural networks are more difficult to t..
wandukong.tistory.com
ResNet (Deep Residual Learning for Image Recognition) 논문 리뷰
논문 제목 : Deep Residual Learning for Image Recognition 오늘은 Deep Residual Learning for Image Recognition에서 마이크로소프트팀이 소개한 ResNet에 대해 다뤄보려 한다. ResNet은 수학적으로 어려운 개..
phil-baek.tistory.com
'Paper Review' 카테고리의 다른 글
| [FCN] Fully Convolutional Networks for Semantic Segmentation (0) | 2023.03.31 |
|---|---|
| [Transformer] Attention Is All You Need (2) (0) | 2023.03.24 |
| [Transformer] Attention Is All You Need (1) (0) | 2023.03.23 |
| [R-CNN] Rich feature hierarchies for accurate object detection and semantic segmentation 정리 (2) | 2023.03.16 |
| [AlexNet] ImageNet Classification with Deep Convolutional Nerual Networks 정리 (0) | 2022.01.28 |
ResNet
마이크로소프트 팀이 개발한 ResNet은 잔차(Residual) 라는 개념을 도입하였고, 그 결과 ILSVRC 2015에서 1위를 차지하였다.
Abstract
- 딥러닝에서 신경망(Neural Network)이 깊을수록 Train은 더 어려워집니다. (오버 피팅이 발생할 확률이 높다.)
- 그래서 ResNet 에서는 깊은 신경망에서도 training을 용이하게 하기 위한 residual learning framework(잔차 학습) 를 제시합니다.
- 함수를 새로 만드는 방법 대신 residual function(잔차 함수)을 train에 사용하는 것으로 Layer를 재구성 합니다.
- ResNet의 residual 네트워크는 optimize를 더 쉽게 하고, 더 깊은 모델에서도 상당한 accuracy를 얻는 것을 empirical evidence showing(경험적으로 보여줍니다).
- 결과적으로 152개의 Layer를 쌓아 기존의 VGG Net 보다 좋은 성능을 내면서 복잡성을 주였고, ILSVRC 2015에서 1등을 하였습니다.
Introduction
- Deep Convolutional Neural Networks 는 이미지 분류 분야에서 중요한 돌파구가 되었습니다.
- 최근 자료들을 통해 네트워크의 깊이가 중요한 요소이며 ImageNet에서 깊은 모델들이 좋은 결과를 낸다는 것을 보여주고 있습니다.
- 이 논문의 저자는 “과연 더 많은 Layer를 쌓는 것만큼 Network의 성능은 좋아질까 ?” 라는 의문을 가졌습니다. 왜냐하면 이와 관련해서 악명 높은 많은 문제 problem of vanishing / exploding gradients 가 발생하기 때문입니다. 이러한 문제는 SGD 와 backpropagation를 적용한 첫 10개의 Layer에서는 normalized initialization, intermediate normalization Layers 를 통해 대부분 해소 되었습니다.
- 하지만 네트워크 깊이가 증가할수록, accuracy가 감소되는 degradation 이 발생한다.
- \(\rightarrow\) 네트워크의 깊이가 깊어짐에 따라 정확도가 포화하고, 급속하게 감소하는 것
- \(\rightarrow\) Overfitting과 다르게 단지 더 많은 Layer들이 추가 되어서이기 때문인데 이러한 근거는 train error, test error 둘 다 높다는 것을 보고 확인할 수 있습니다.

- 이 문제는 모든 시스템들이 optimize 하기 쉽지 않다는 것을 보여주기 때문에 얕은 구조와 더 깊은 아키텍처를 비교해 보여주려고 합니다.
- Identity mapping layer 를 추가해봤지만 실험을 통해 좋은 solution이 아니라는 결과를 얻었습니다.
- 그래서 ResNet 에서는 Deep residual learning framework 라는 개념을 도입하여 degradation 문제를 해결하려고 합니다.
- 추가된 Layer가 identity mapping이고, 추가되지 않은 다른 레이어들은 더 얕은 모델에서 학습된 Layer를 사용하는 것
- \(\rightarrow\) 쌓여진 Layer가 desired underlying mapping에 바로 적용되는 것이 아니라 residual mapping에 적용하도록 한다.
기존의 네트워크는 입력 \(x\)를 받고 Layer를 거쳐 타겟값 \(y\)로 mapping 하는 함수 \(H(x)\)를 얻는 것이 목적이면, Residual Learning은 출력과 입력의 차인 \(H(x)-x\)를 얻도록 목표를 수정하는 것입니다. 이는 nonlinear layer(비선형 적인) mapping \(F(x)=H(x)-x\)를 최소화시켜야 하고 이는 출력과 입력의 차이를 줄인다는 의미가 됩니다.
여기서 입력 \(x\)의 값은 변경할 수 없으므로 \(F(x)\)가 0이 되는 것이 최적의 해이고, 결국 \(H(x)=x\)가 되는 \(H(x)\)를 \(x\)로 mapping 하는 것이 학습의 목표가 됩니다.
이를 전개하면 \(H(x)=F(x)+x\)의 형태가 됩니다. \(\rightarrow\) residual mapping이 기존 mapping 보다 optimize 하기 쉽다는 것을 가정합니다. 그러한 이유는 이전에는 Unreferenced mapping인 알지 못하는 최적의 값으로 \(H(x)\)를 근사하도록 학습시켜야 한다는 점 때문에 어려움이 있었는데, \(H(x)=x\) 라는 최적의 목표값이 사전에 제공되기 떄문에 Identity mapping인 \(F(x)\)가 학습이 더 쉬워지기 때문입니다.
결과적으로 \(H(x)=F(x)+x\)는 Shortcut Connection과 동일한데 이는 하나 또는 하나 이상의 Layer를 Skip 가능하게 만들어 줍니다. \(\rightarrow\) 단순히 입력에서 출력으로 바로 연결되는 shortcut만 추가하면 되기 떄문이다.
ResNet에서는 Shortcut Connection을 위해 identity mapping을 수행하고, 그 결과는 stacked layer의 output에 더해집니다.
ResNet에서는 출력과 입력 간의 차에 대해 학습을 시키면 해결 할 수 있다고 생각하였습니다.
\(\rightarrow\) 입력 \(x\)값을 출력 \(F(x)\)에 더하는 identity mapping (Shortcut Connections)

\(F(x) = W_2 \times ReLU(W_2 \times x)\)
만약 \(F(x)\)와 \(x\)가 차원이 다를 경우, \(W_s\) projection matrix를 곱하여 차원을 같게 만든 후 더함.
\(\rightarrow\) \(y = F(x) + W_s \times x\)
이 Identity Shortcut Connection 은 추가적인 parameter도 필요하지 않고 복잡한 곱셈 연산도 필요하지 않는 것이 장점입니다. \(\rightarrow\) 곱셈 연산에서 덧셈 연산으로 변형되어 몇 개의 Layer를 건너뛰는 효과를 가지고 있습니다.
이를 이용한 네트워크는 backpropagation, SGD 로 end-to-end 학습이 가능하며, solver 수정없이 common library 를 이용하여 쉽게 구현이 가능하다.
ResNet은 실험적인 방법을 통해 degradation 문제를 보이고 논문의 방법을 평가합니다.
\(\rightarrow\) PlainNet과 달리 ResNet이 optimize 하기 더 쉽다.
\(\rightarrow\) ResNet은 Depth가 증가해도 더 쉽게 accuracy를 얻을 수 있다.
Related Work
- Residual Representations
- Shortcut Connections
\(\rightarrow\) ResNet 에서 사용한 Identity shortcut 기법의 장점인 parameter 필요 X & 복잡한 곱셈 연산 필요 X 등을 언급하였다.
Deep Residual Learning
Residual Learning
\(H(x)\) : original mapping, \(F(x)\) : residual mapping, \(F(x)+x\) : original function
앞서 Introduction에서 설명한 것을 다시 얘기합니다.
만약 residual learning의 재구성을 통해, residual mapping이 optimal(최적) 인 경우 solver는 단순히 residual mapping에 접근하기 위해 multi nonlinear layers의 weight 를 얻기가 더 쉬울 것입니다.
\(\rightarrow\) 실제로는 Identity mapping이 최적일 가능성이 낮다고 합니다. 하지만 ResNet에서 제안하는 재구성 방식은 문제에 preconditioning을 추가하는데 도움을 줍니다 따라서 preconditioning으로 인해 optimal function이 zero mapping보다 identity mapping에 더 가깝다면, solver가 identity mapping을 참조하여 작은 변화를 학습하는 것이 새로운 function을 학습하는 것보다 더 쉬울 것이라고 본 논문에서 주장한다.
정리하자면, 재구성한 식 \(F(x)+x\)는 identity mapping이 optimal 일 경우를 가정하여 구성한 것으로 보인다. 그러나, 이는 가정일 뿐 실제로 depth가 깊어질수록 성능의 향상을 기대하는 경우엔 \(H(x)\)의 optimal이 identity라고 보기 어렵다.
그럼에도 \(F(x)+x\) 라는 식에서는 입력 x가 학습 시에 일종의 guide 로써 적용하여 학습을 도와주므로, identity가 optimal이 아닌 경우라도 이 재정의 은 여전히 긍정적인 효과를 기대할 수 있을 것이다. [참고]
Identity Mapping by Shortcut
ResNet에서는 모든 stacked layers 에 residual learning 을 적용한다. 다음 그림의 building block 을 다음과 같이 정의한다.

[Enq. 1] \(y=F(x, \{W_i\})+x\)
\(\rightarrow\) \(F(x, \{W_i\})\) : 학습 될 residual mapping (\(x\) : input, \(y\) : output)
\(\rightarrow\) 위 그림과 같이 Layer가 2개인 경우 \(F=W_2 \sigma(W_1 \times x)\)로 나타낼 수 있다. (\(\sigma\) : ReLU, \(bias\) : 생략)
\(\rightarrow\) \(F+x\) 연산은 shorcut connection, element-wise addition으로 수행되며, addition 후 second nonlinearity로 ReLU를 적용한다.
\(\rightarrow\) parameter도 없고 계산 복잡도도 없다.
\(\rightarrow\) 위 수식에서는 \(x\)와 \(F\)의 차원이 같을 것
[Enq. 2] \(y=F(x, \{W_i\}) + W_s \times x\)
\(\rightarrow\) [Enq. 1] 에서 \(F + x\) 연산은 2개의 차원이 같아야 한다. 동일하지 않다면 이를 위해 linear projection \(W_s\)를 적용할 수 있다.
\(\rightarrow\) [Enq. 1] 에서 square matrix로 \(W_s\)를 수용할 수 있지만, 성능 문제를 해결하기 위해 identity mapping 만으로도 충분하고 경제적이므로 \(W_s\)는 dimention matching 용도로만 사용한다.
[추가]
위 식을 conv Layer 상에서도 마찬가지로 identity mapping을 구현할 수 있다.
이 경우에는 dimension matching을 위해 \(1\times 1\) filter의 conv Layer를 이용하며, element-wise addition은 feature map 간의 channel-by-channel addition으로 수행된다.


Network Architectures
ResNet 에서는 다양한 형태의 plain/residual network에 대해 테스트 했으며, 일관된 현상을 관찰하였습니다.
테스트에서 사용할 ImageNet dataset을 위한 두 모델은 다음과 같이 정의합니다.
plain network
- baseline은 주로 VGGNet 에 영감을 얻어 만들어 졌으며 conv layer는 대게 \(3\times 3\) filter를 가지며
- 동일한 output feature map size에 대해, layer는 동일한 수의 filter를 갖는다.
- feature map size가 절반이 될 경우, layer당 time complexity를 보전하기 위해 filter의 수를 2배로 한다.
- conv layer는 stride 2로 downsampling(Pooling) 하며, network는 global average pooling layer와 softmax를 사용한 1000-way FC layer로 끝난다.
- plain network는 VGG-19 에 비해 적은 수의 filter와 낮은 complexity를 가진다.
residual network
- plain network 기반으로 shortcut connection을 삽입하여 residual version의 network를 만든다.
- identity shortcut [Eqn. 1]은 input과 output이 동일한 dimension인 경우(실선) 직접 사용될 수 있으며, dimension이 증가하는 경우(점선) 아래 두 옵션을 고려한다.
- zero padding을 추가로 하여 dimension matching 후 identity mapping 수행
- [Eqn. 2]의 projection shortcut을 dimention matching에 사용
- shortcut connection이 다른 크기의 feature map 간에 mapping 될 경우, 두 옵션 모두 stride 2로 수행. (feature map의 크기가 달라지는 경우는 stride가 2인 con layer를 통한 downsampling을 거쳤기 떄문)

Implementation
논문에서 ImageNet dataset에 대한 실험은 AlexNet과 VGG의 방법을 따른다.
이미지는 scale augmentation를 위해 [256,480]에서 무작위하게 샘플링 된 shorter side를 사용하여 rescaling 된다.
\(244\times 244\) crop 은 horizontal flip with per-pixel mean subtracted 이미지 중에 무작위로 샘플링 되며, standard color augmentation도 사용된다.
- 각각의 conv layer와 activation 사이에는 batch normalization을 사용하며, He initialization 기법으로 weigth를 초기화하여 모든 plain/residual network을 학습한다.
- batch normalization에 근거해 dropout을 사용하지 않는다.
- learning rate는 0.1 에서 시작하여 error가 안정된 상태가 되면 learning rate를 10으로 나누어 적용하며, decay는 0.0001, momentum은 0.9로 한 SGD를 사용하였다.
- mini-batch size 는 256로 했으면, iteration은 총 600K회 수행된다.
Experiments
ImageNet Classification
ResNet 에서는 1000개의 class로 구성 된 ImageNet 2012 classification dataset에서 제안하는 방법을 평가했습니다.


Plain Networks
먼저 18-Layer 및 34-Layer plain network를 평가합니다.
그 결과 plain에서는 18-Layer network에 비해, 34-Layer network의 validation error가 높은 것으로 보입니다.
34-layer plain network의 error가 학습 과정 전반에 걸쳐서 더 높게 나타나는 성능 저하 문제를 확인할 수 있습니다.
논문의 저자들은 여기서 직면하는 optimization difficulty가 vanishing gradients에 의한 것 같지는 않다고 주장합니다.
그 이유는 plain network가 batch normalizaion을 포함하여 학습했기 때문에 forward propagated signal의 분산이 0이 아니도록 보장했으며, backward propagation gradients가 healty norm을 보이는 것도 확인했기 때문입니다. 따라서 gradient vanishing 문제는 발생하지 않았다고 볼 수 있습니다.
다음 결과에 따르면 34-layer plain network가 여전히 경쟁력 있는 정확도를 달성했으며, 이는 solver의 작동이 이루어지긴 한다는 것을 의미한다. 그래서 저자들은 deep plain network는 exponentially low convergence rate를 가지며, 이것이 training error의 감소에 영향을 끼쳤을 거라 추측한다.

Residual Networks
다음으로 18-Layer 및 34-Layer residual network(ResNet)을 평가한다.
baseline architecture은 plain network와 동일하며, 각 \(3 \times 3\) filter pair에 shortcut connection을 추가했다. 모든 shortcut connection은 identity mapping을 사용하며, dimension matching을 위해서는 zero-padding을 사용한다. 따라서 대응되는 plain network에 비해 추가되는 parameter가 없다.
[Table. 2]와 결과 그림에서 알 수 있는 3가지 주요 관찰 결과는 다음과 같다.
- residual learning으로 인해 상황이 바뀌었다. 34-layer ResNet이 18-layer ResNet 보다 우수한 성능을 보인다. 또한, 34-layer ResNet이 상당히 낮은 training error를 보였으며, 이에 따라 상향된 validation 성능이 관측됐다. 이는 성능 저하 문제가 잘 해결됐다는 것과, 증가된 depth에서도 합리적인 accuracy를 얻을 수 있다는 것을 나타낸다.
- 34-layer ResNet은 이에 대응하는 plain network와 비교할 때, validation data에 대한 top-1 error를 3.5% 줄였다.
- 18-layer plain과 residual network 간에는 유사한 성능을 보였지만, 결과 그림에서 보듯 18-layer ResNet은 더욱 빠르게 수렴한다. 이는 network가 not overly deep 한 경우 plain network에서도 좋은 solution을 찾을 수 있다는 것으로 볼 수 있다.
Identity vs Projection Shortcut
위 [Table. 3] 에서는 다음 3가지 옵션에 대한 결과를 보여준다.
(A) zero-padding shortcut는 dimension matching에 사용되며, 모든 shortcut은 parameter-free로 한 경우
(B) projection shortcut는 차원을 늘릴 때만 사용되며, 다른 shortcut은 모두 identity로 한 경우
(C) 모든 shortcut을 projection으로 한 경우
3가지 옵션들은 모두 plain network보다 훨씬 나은 결과를 보여준다. 성능은 C > B > A 순서로 좋았다.
A 의 zero-padding 과정에 residual learning이 없어서 B 가 더 나은 성능을 보이고
C의 추가 parameter 가 많은 projection shortcut에 의해 B 보다 더 나은 성능을 보인다.
여기서 3가지 옵션 간의 차이는 미미한 것으로 보아 projection shortcut이 degradation problem을 해결하는데 필수적이지 않다는 것을 알 수 있다. 그래서 이 뒤부터는 메모리, 시간, 복잡성, 모델 크기 감소를 위해 옵션 (C)를 사용하지 않는다.
Identity shortcut은 아래에서 설명될 bottleneck architectures의 복잡성을 증가시키지 않는 점에서 특히 중요하다.
Deeper Bottleneck Architectures.
감당할 수 없는 training time에 대한 우려로 인해, buliding block을 bottleneck design으로 수정한다.
다음 그림처럼 각 residual function F, 2-layer stack 대신 3-layer stack을 사용한다.

3개의 layer는 각각 순서대로 \(1\times 1, 3\times3, 1\times1\) conv layer 이며, \(1\times1\) conv layer는 dimension을 줄이거나 늘리는 용도로 사용하며, \(3\times3\) layer의 input/output의 dimension을 줄인 bottlenet으로 둔다.
여기서 parameter free인 identity shortcut은 이 architecture에서 특히 중요하다. 만약 위 그림의 오른쪽 다이어그램에서 identity shortcut이 projection으로 대체된다면, shortcut이 두 개의 high-dimensional 출력과 연결되므로 time complexity와 model size가 두 배 늘어난다. 따라서 identity shortcut은 이 bottleneck design을 보다 효율적인 모델로 만들어 준다.
50-Layer ResNet
34-layer ResNet의 2-layer block 들을 3-layer bottleneck block으로 대체하여 50-layer ResNet을 구성하였다. dimention matching을 위해 위의 옵션 (B)를 사용하였다.
\(\rightarrow\) (B) projection shortcut은 dimension을 늘릴 때만 사용되며, 다른 shortcut은 모두 identity다.
101-Layer and 152-Layer ResNet
여기에 3-layer bottleneck block을 추가하여 101-layer 및 152-layer ResNet을 구성했다. depth가 상당히 증가했음에도 상당히 높은 정확도가 결과로 나왔다.
Comparison with State-of-the-art Methods

6가지 모델을 앙상블 기법을 적용하여 실험 결과 ResNet이 3.57% top-5 error를 달성하며, ILSVRC 2015에서 1등을 하였다.
CIFAR-10 and Analysis
CIFAR-10 dataset을 대상으로 모델 학습 및 검증 결과를 다룬다.
Analysis of Layer Responses.

Plain/Residual Network의 각 layer responses의 표준편차를 보여준다. ResNet의 response가 plain network보다 적은걸 볼 수 있는데, 이는 residual function이 non-residual function보다 일반적으로 0에 가까울 것이라는 저자들의 basic motivation을 뒷바침한다.
Exploring Over 1000 Layers

1202-layer network는 110-layer network와 비슷한 training error를 보이지만 test는 좋지 못하였는데 overfitting이 발생한 것 같다고 말한다.
참조 사이트
https://sike6054.github.io/blog/paper/first-post/
(ResNet) Deep residual learning for image recognition 번역 및 추가 설명과 Keras 구현
Paper Information
sike6054.github.io
[논문 리뷰] Deep Residual Learning for Image Recognition - ResNet(1)
ResNet ResNet 이라는 이름으로 더 유명한 논문을 리뷰해보겠습니다. 최고의 빅데이터 분석 동아리 '투빅스' 과제 겸사겸사 하는 리뷰입니다. (사실 이게 아니라 구현 과제를 해야되는데 어렵네요...
jxnjxn.tistory.com
https://wandukong.tistory.com/18
[논문 리뷰] ResNet 논문 리뷰
오늘은 최근에 읽은 유명한 논문, ResNet을 리뷰해보려고 합니다. 논문 링크 : https://arxiv.org/abs/1512.03385 Deep Residual Learning for Image Recognition Deeper neural networks are more difficult to t..
wandukong.tistory.com
ResNet (Deep Residual Learning for Image Recognition) 논문 리뷰
논문 제목 : Deep Residual Learning for Image Recognition 오늘은 Deep Residual Learning for Image Recognition에서 마이크로소프트팀이 소개한 ResNet에 대해 다뤄보려 한다. ResNet은 수학적으로 어려운 개..
phil-baek.tistory.com
'Paper Review' 카테고리의 다른 글
| [FCN] Fully Convolutional Networks for Semantic Segmentation (0) | 2023.03.31 |
|---|---|
| [Transformer] Attention Is All You Need (2) (0) | 2023.03.24 |
| [Transformer] Attention Is All You Need (1) (0) | 2023.03.23 |
| [R-CNN] Rich feature hierarchies for accurate object detection and semantic segmentation 정리 (2) | 2023.03.16 |
| [AlexNet] ImageNet Classification with Deep Convolutional Nerual Networks 정리 (0) | 2022.01.28 |
