Attention Is All You Need
해당 글과 그림의 출처는 lllustrated Transformer과 lllustrated Transformer(번역)을 참고하였습니다.
Positional Encoding을 이용해서 Sequence(시퀀스)의 순서 나타내기
RNN이 자연어 처리에서 유용했던 이유는 단어의 위치에 따라 단어를 순차적으로 입력받아서 처리하는 RNN의 특성으로 인해 각 단어의 위치 정보(Position Information)를 가질 수 있다는 점에 있었습니다.
하지만 Transformer 모델에서는 입력 문장에서 단어들의 순서에 대해서 고려하고 있지 않으므로 단어의 위치 정보를 다른 방식으로 알려줄 필요가 있습니다.
이를 위해서, Transformer 모델은 각각의 입력 embedding에 "positional encoding"이라고 불리는 하나의 벡터를 추가합니다. 이 벡터들은 모델이 학습하는 특정한 패턴을 따르는데, 이러한 패턴은 모델이 각 단어의 위치와 시퀀스 내의 다른 단어 간의 위치 차이에 대한 정보를 알 수 있게 해줍니다. 이 벡터들을 추가하기로 한 배경에는 이 값들을 단어에 embedding에 추가하는 것이 나중에 query/key/value 벡터들로 투영되었을 때 단어들 간의 거리를 늘릴 수 있다는 점 때문입니다.
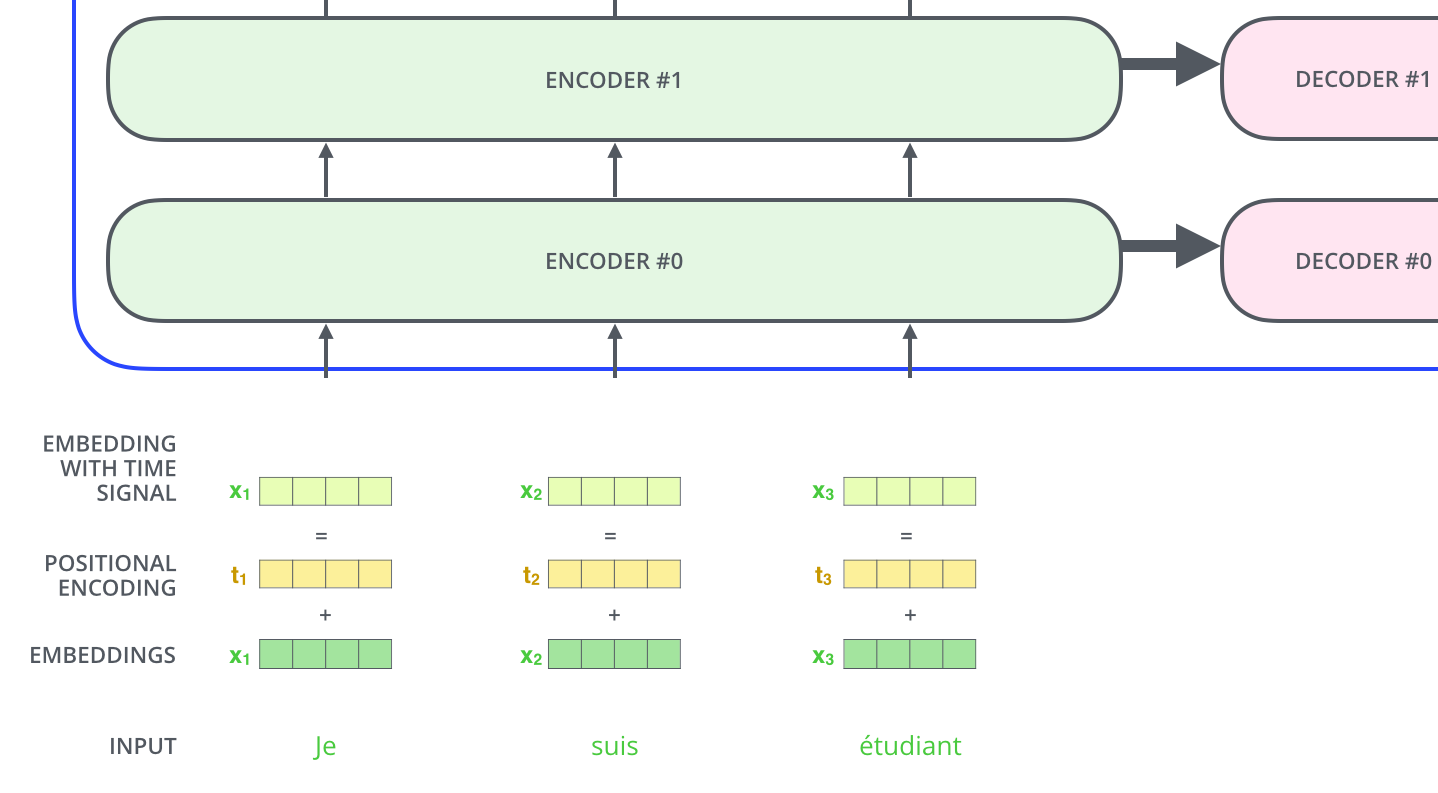
모델에게 단어의 순서에 대한 정보를 주기 위하여, 위치 별로 특정한 패턴을 따르는 positional encoding 벡터들을 추가합니다.
만약 embedding의 사이즈가 4라고 가정한다면, 실제로 각 위치에 따른 positional encoding은 다음과 같은 것입니다.
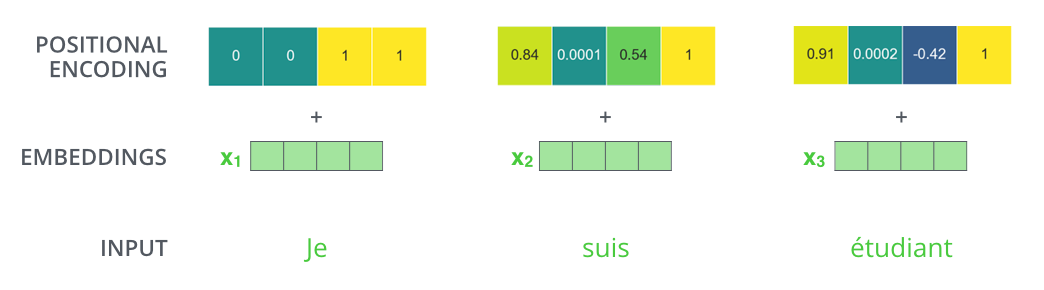
positional encoding 값들은 다음 두 개의 함수를 사용해서 구합니다.
$$ PE(pos, 2i) = sin(pos/10000^{2i/d_{model}}) $$
$$ PE(pos, 2i+1) = cos(pos/10000^{wi/d_{model}})$$
\(sin\)함수와 \(cos\)함수의 그래프를 상기해보면 요동치는 값의 형태를 생각할 수 있는데, transformer는 이 값들을 임베딩 벡터에 더해주므로서 단어의 순서 정보를 더하여 줍니다.
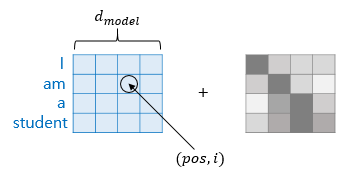
위 함수 식에서 \(pos\)는 입력 문장에서의 임베딩 벡터의 위치를 나타내며, \(i\)는 임베딩 벡터 내의 차원의 인덱스를 의미합니다. (임베딩 벡터 내의 각 차원의 인덱스가 짝수면 \(sin\), 홀수면 \(cos\) 함수의 값 사용)
위와 같은 positional encoding 방법을 사용하면 순서 정보가 보존되는데, 예를 들어 각 임베딩 벡터에 positional encoding 값을 더하면 같은 단어라고 하더라도 문장 내의 위치에 따라서 transformer의 입력으로 들어가는 임베딩 벡터의 값이 달라집니다.
다음 그림에서 각 행은 하나의 벡터에 대한 positional encoding에 해당합니다. 그러므로 첫 번째 행은 우리가 입력 문장의 첫 번째 단어의 embedding 벡터에 더할 positional encoding 벡터입니다.
각 행은 512개의 셀을 가진 벡터이며 각 셀의 값은 -1과 1 사이를 가집니다. 다음 그림은 이 셀들의 값들에 대해 색깔을 다르게 나타내어 positional encoding 벡터들이 가지는 패턴을 볼 수 있도록 시각화 하였습니다.
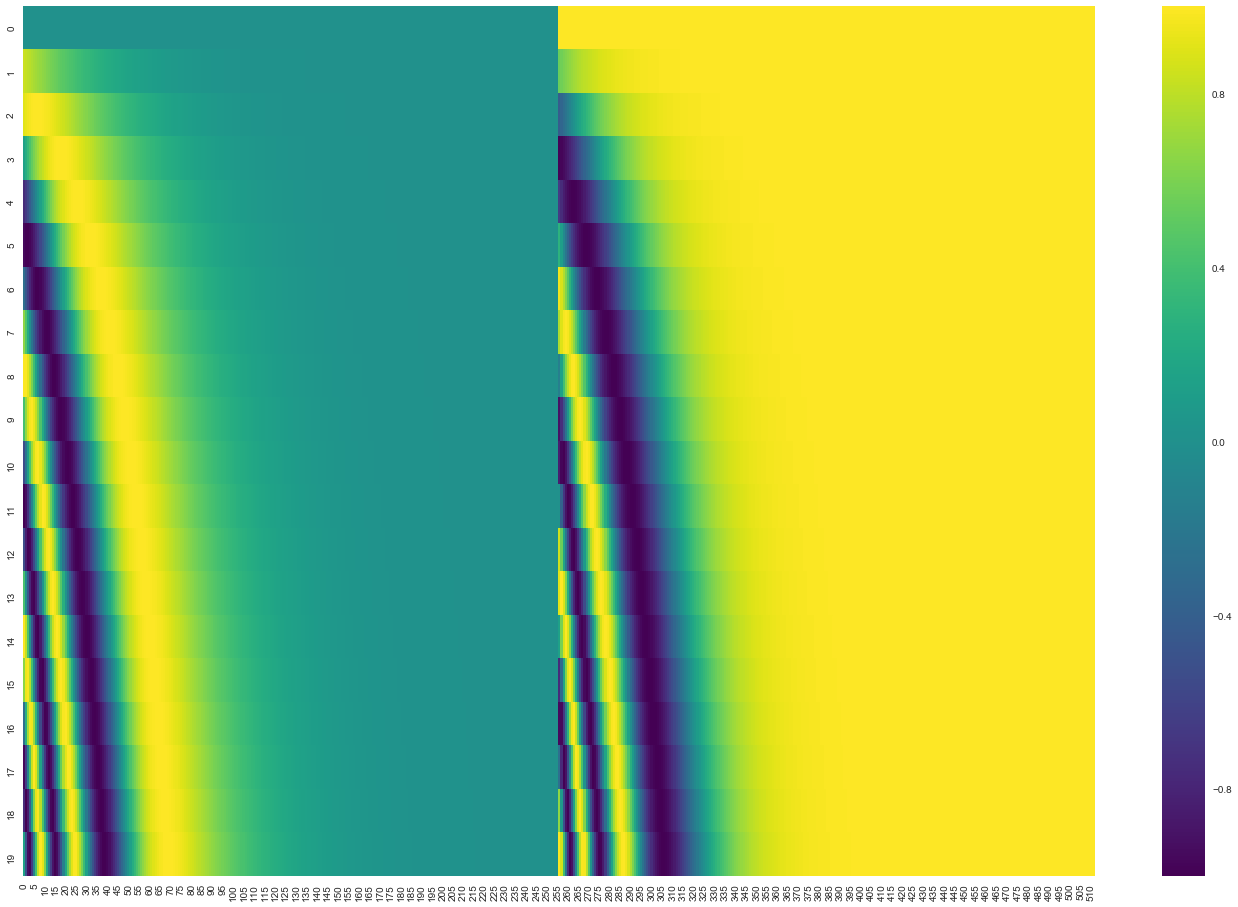
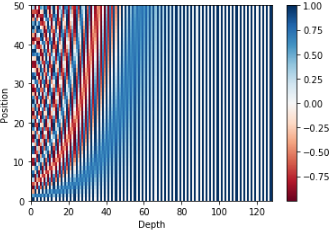
20개의 단어와 그의 크기 512인 embedding에 대한 positional encoding의 실제 예시입니다. 위 그림에서 볼 수 있듯이 이 벡터들은 중간 부분이 반으로 나눠져 있습니다. 그 이유는 바로 왼쪽 반은(256) \(sin\) 함수에 의해서 생성되었고, 나머지 오른쪽 반은 또 다른 함수인 \(cos\) 함수에 의해 생성되었기 때문입니다. 그 후 이 두값은 연결되어 하나의 positional encoding 벡터를 이루고 있습니다.
본 논문에서 이러한 방법은 본 적이 없는 길이의 시퀀스에 대해서도 positional encoding을 생성할 수 있기 때문에 scalability에서 큰 이점을 가진다고 합니다. (예를 들어, 이미 학습된 모델이 자신의 학습 데이터보다도 더 긴 문장에 대해서 번역을 해야 할 때에도 \(sin\)과 \(cos\)으로 이루어진 식은 positional encoding을 생성해낼 수 있습니다.)
The Residuals
Encoder를 넘어가기 전 한 가지를 더 짚자면, 각 encoder 내의 sub-layer가 residual connection으로 연결되어 있으며, 그 후에는 layer-normalization 과정을 거친다는 것입니다.
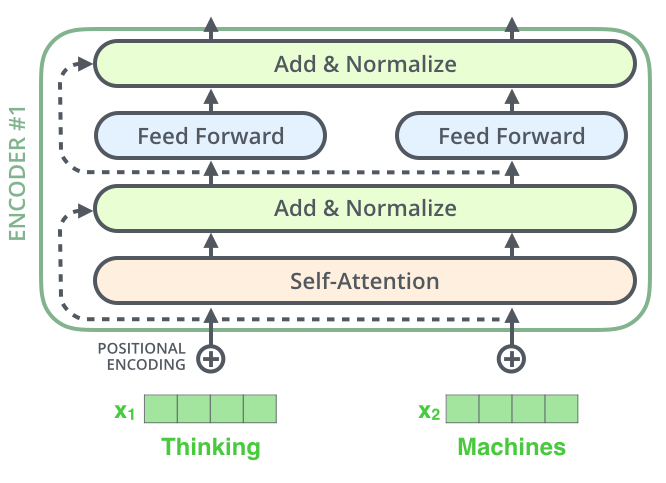
이 벡터들과 layer-normalization 과정을 시각화 한다면 다음과 같습니다.
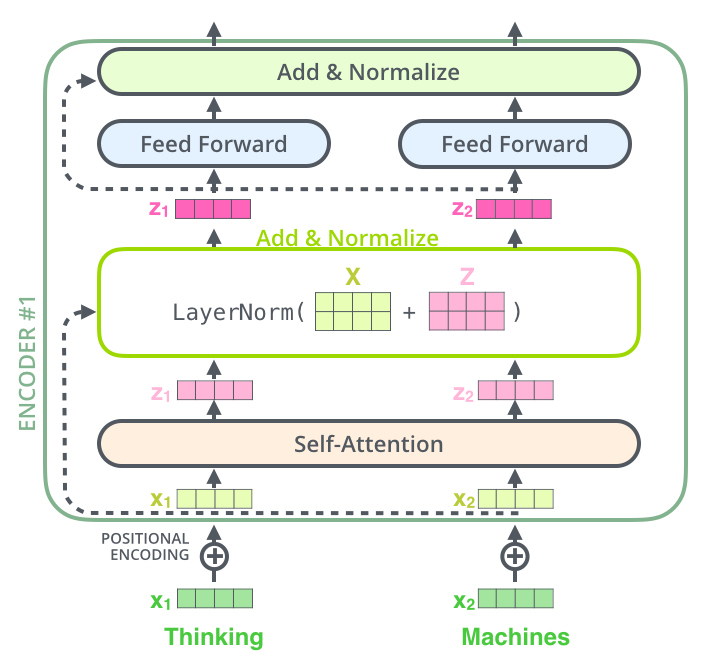
이것은 decoder 내에 있는 sub-layer 들에도 똑같이 적용되어 있습니다. 만약 2개의 encoder와 decoder로 이루어진 단순한 Transformer를 생각한다면 다음과 같습니다.
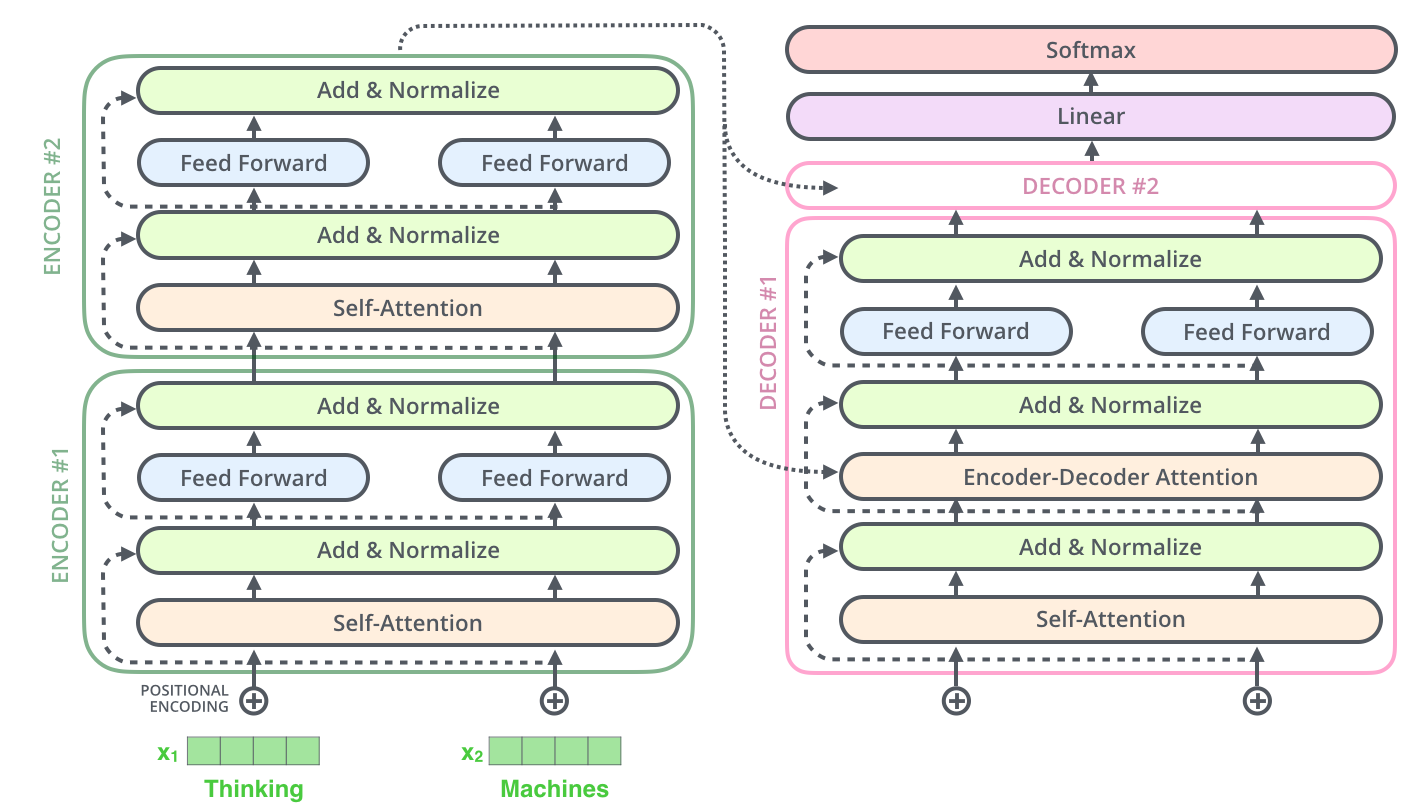
The Decoder Side
Encoder에서 사용되는 대부분의 개념들이 Decoder에도 사용됩니다.
먼저 transformer에서 사용되는 3가지의 Attention에 대해서 간단히 정리해보겠습니다.
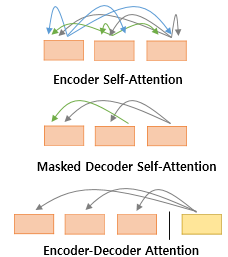
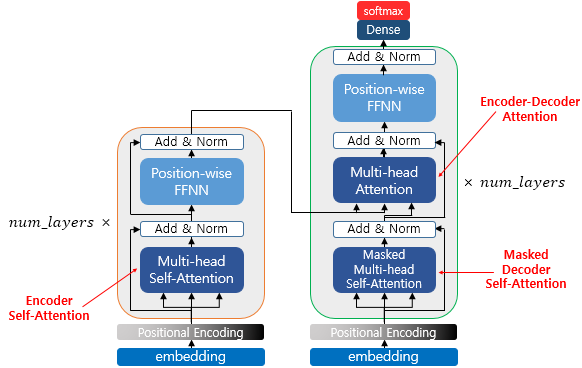
첫 번째 그림인 Self-Attention은 Encoder에서 이루어지지만, 두 번째 그림인 Self-Attention과 세 번째 그림인 Encoder-Decoder Attention은 Decoder에서 이루어집니다. Self-Attention은 본질적으로 Query, Key, Value가 동일한 경우를 말합니다.(벡터의 값이 같은게 아니라, 벡터의 출처가 같다는 의미입니다.) 반면, Encoder-Decoder Attention에서는 Qeury가 Decoder의 벡터인 반면에 Key와 Value가 Encoder의 벡터이므로 Self-Attention이라고 부르지 않습니다.
Encoder의 Self-Attention : Query = Key = Value
Decoder의 Masked-Self-Attention : Query = Key = Value
Decoder의 Encdoer-Decoder Attention : Query - Decoder 벡터 / Key = Value - Encoder 벡터
먼저 Encoder가 입력 시퀀스를 처리하기 시작합니다. 그 다음 가장 윗단의 Encoder의 출력은 Attention 벡터들인 \(K\)와 \(V\)로 변형됩니다. 이 \(K\), \(V\) 벡터들은 이제 각 Decoder의 "Encoder-Decoder Attention" layer 에서 Decoder가 입력 시퀀스에서 적절한 장소에 집중할 수 있도록 도와줍니다.
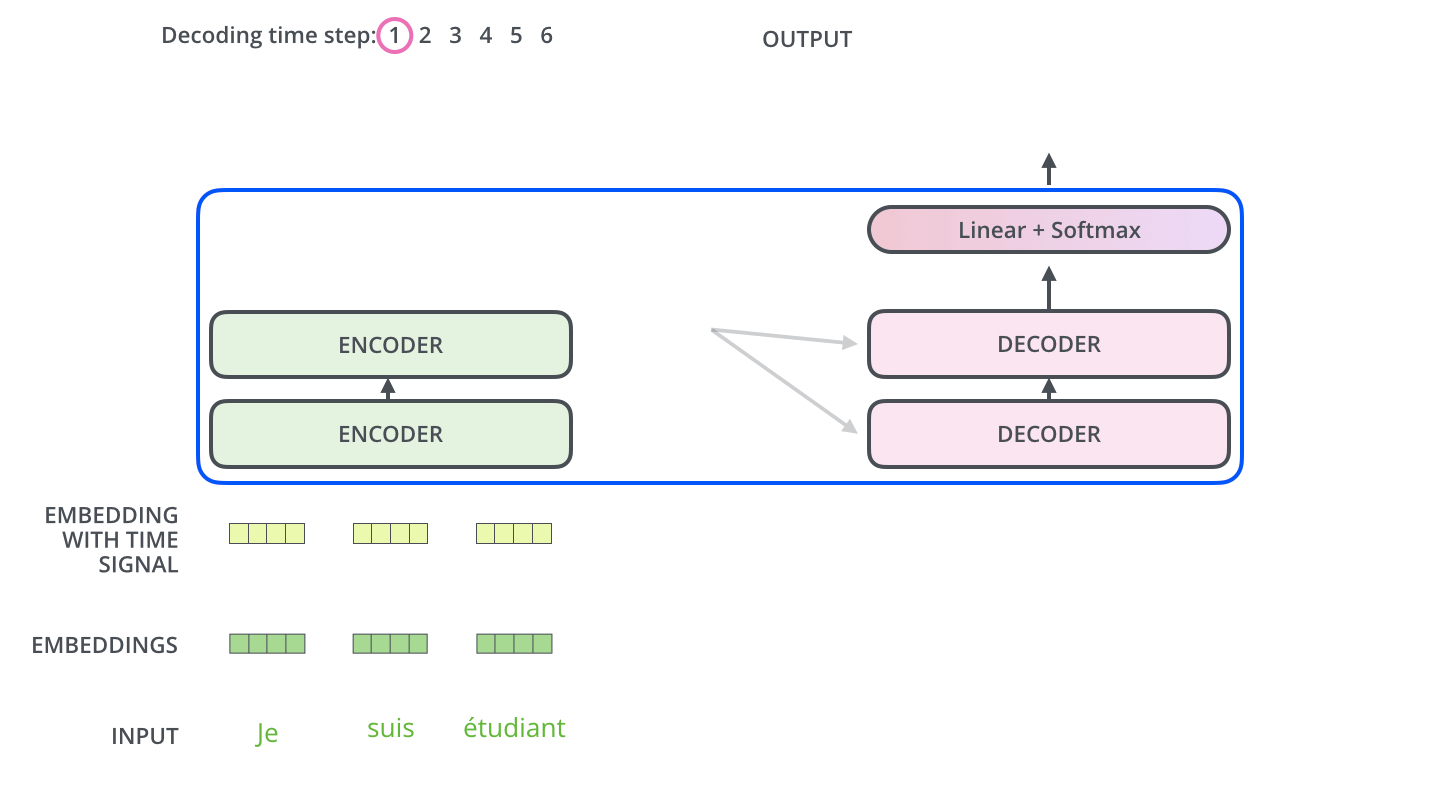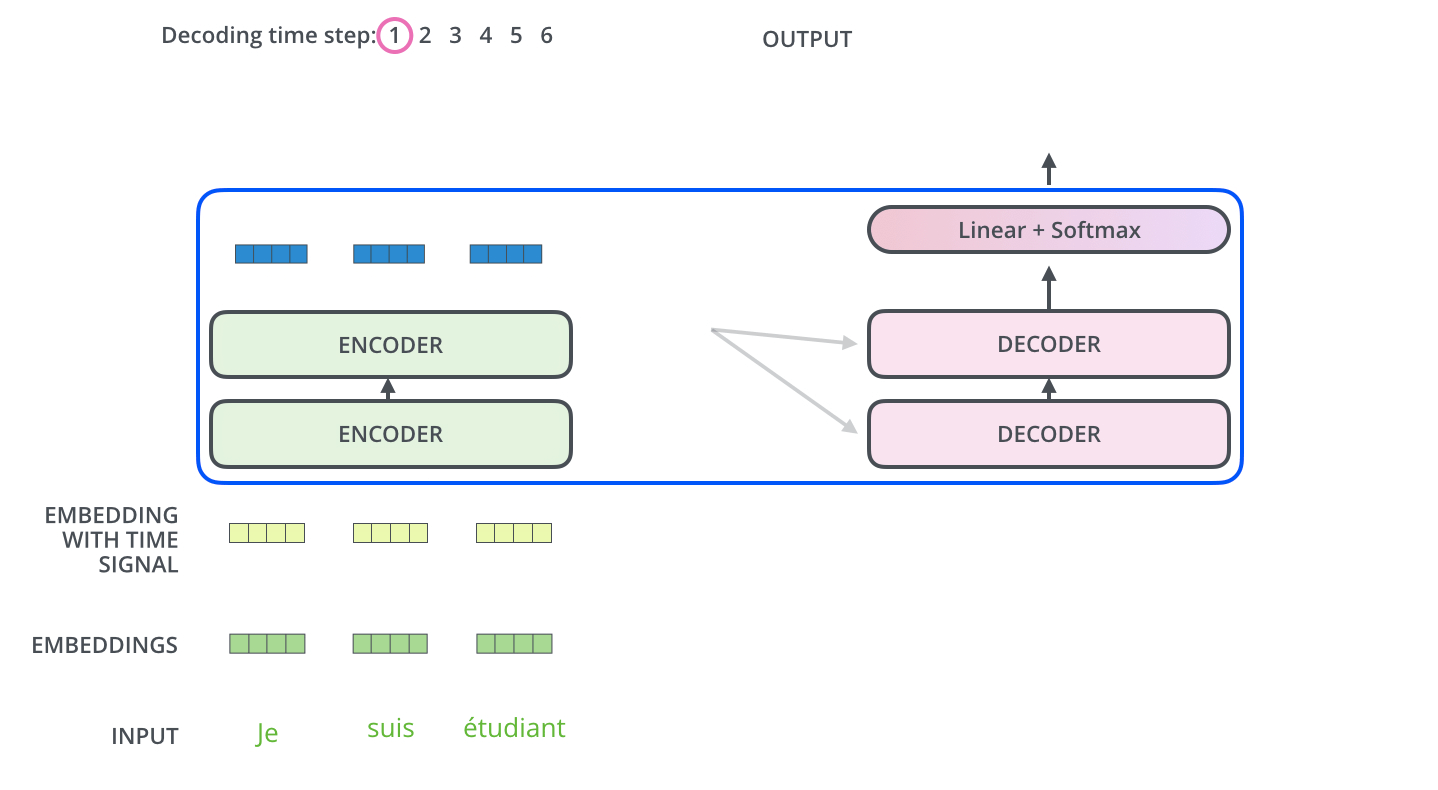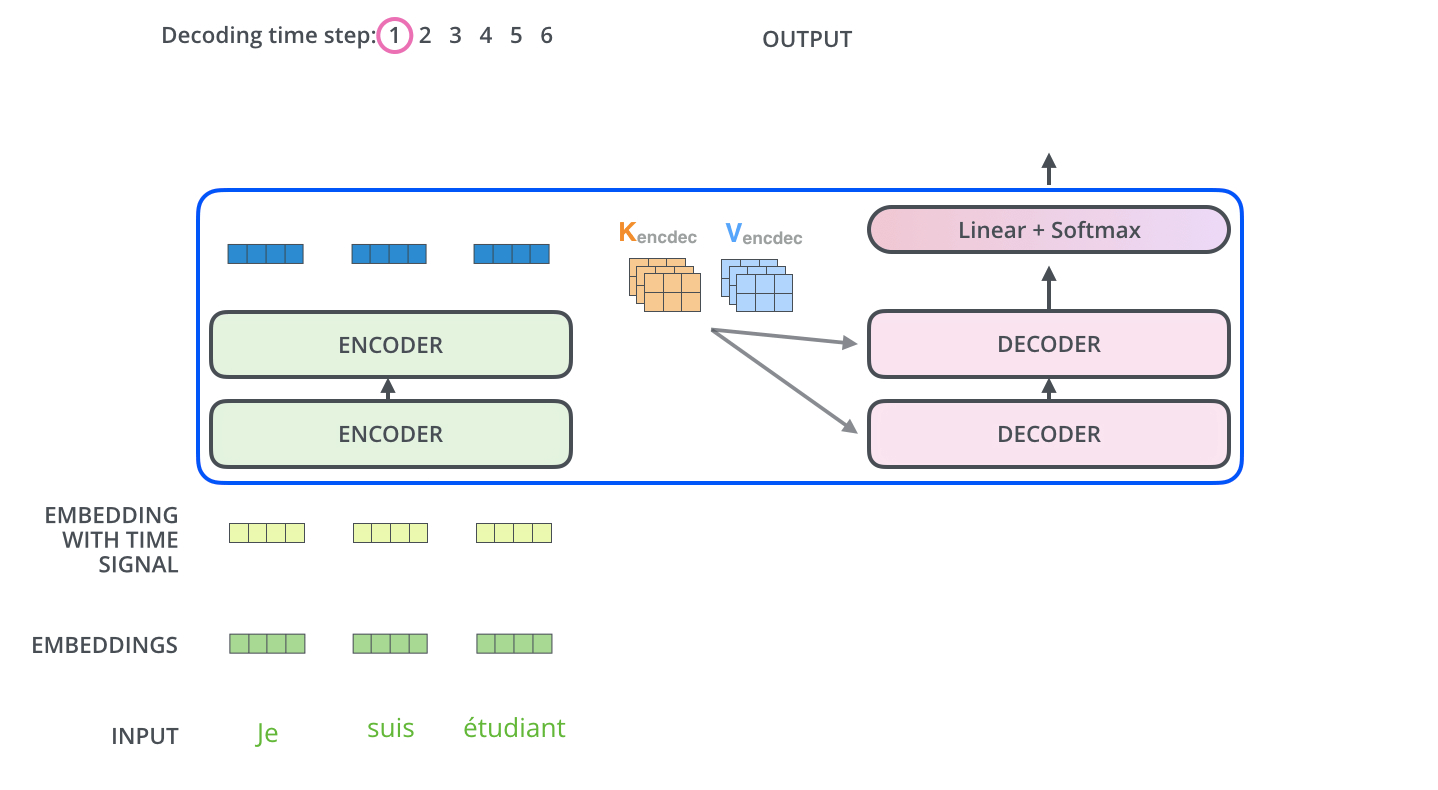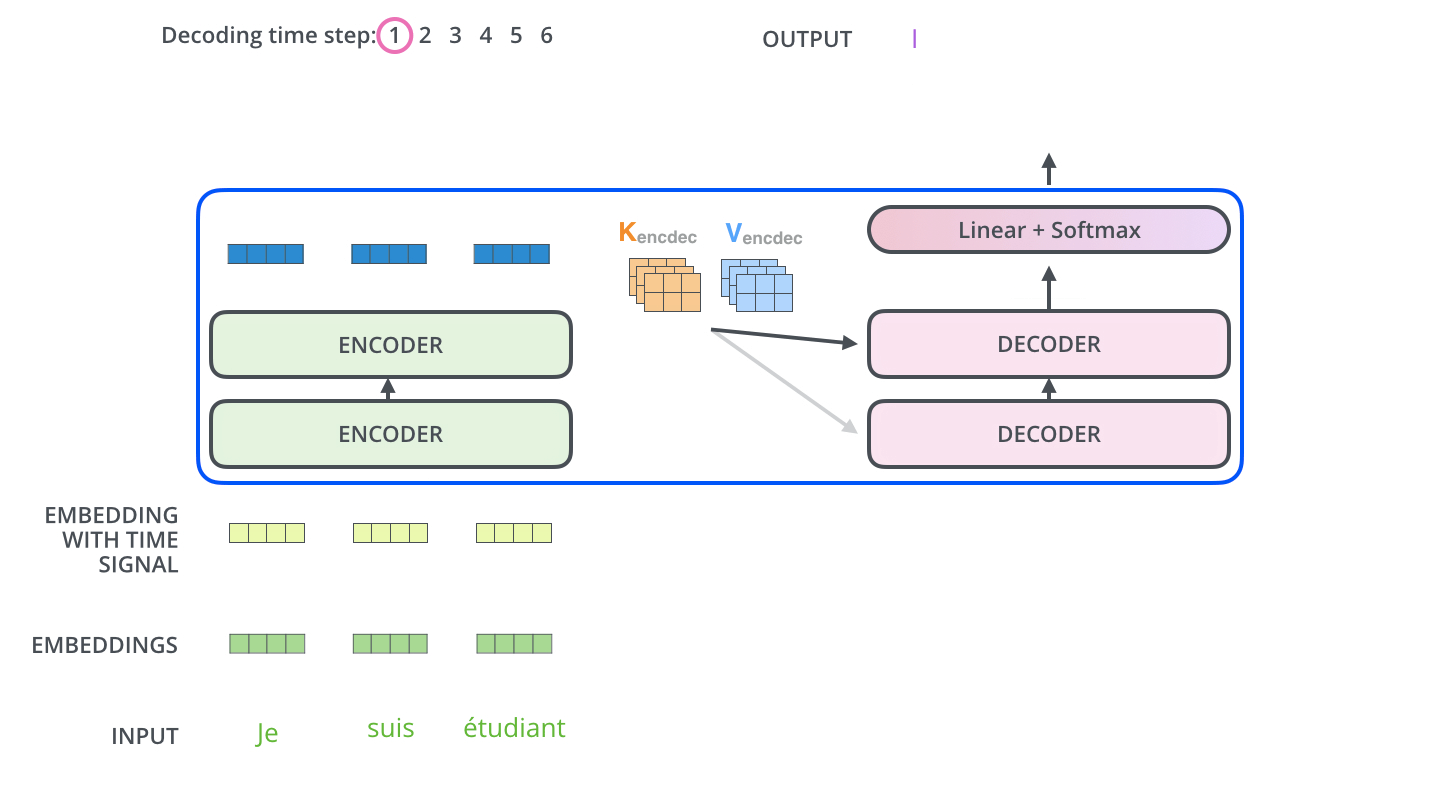
이 단계가 끝나면 Decoding 단계가 시작됩니다. Decoding 단계의 각 step은 출력 시퀀스의 한 element를 출력합니다.
Decoding step은 Decoder가 출력을 완료 했다는 Special 기호인 <End of Sentence>를 출력할 때까지 반복됩니다. 각 setp 마다 출력된 단어는 다음 step의 가장 밑단의 Decoder에 들어가고 Encoder와 마찬가지로 여러 개의 Decoder를 거쳐 올라갑니다. Encoder의 입력에 했던 것과 동일하게 embedding 후, postional encoding을 추가하여 Decoder에게 각 단어의 우치 정보를 더해줍니다.
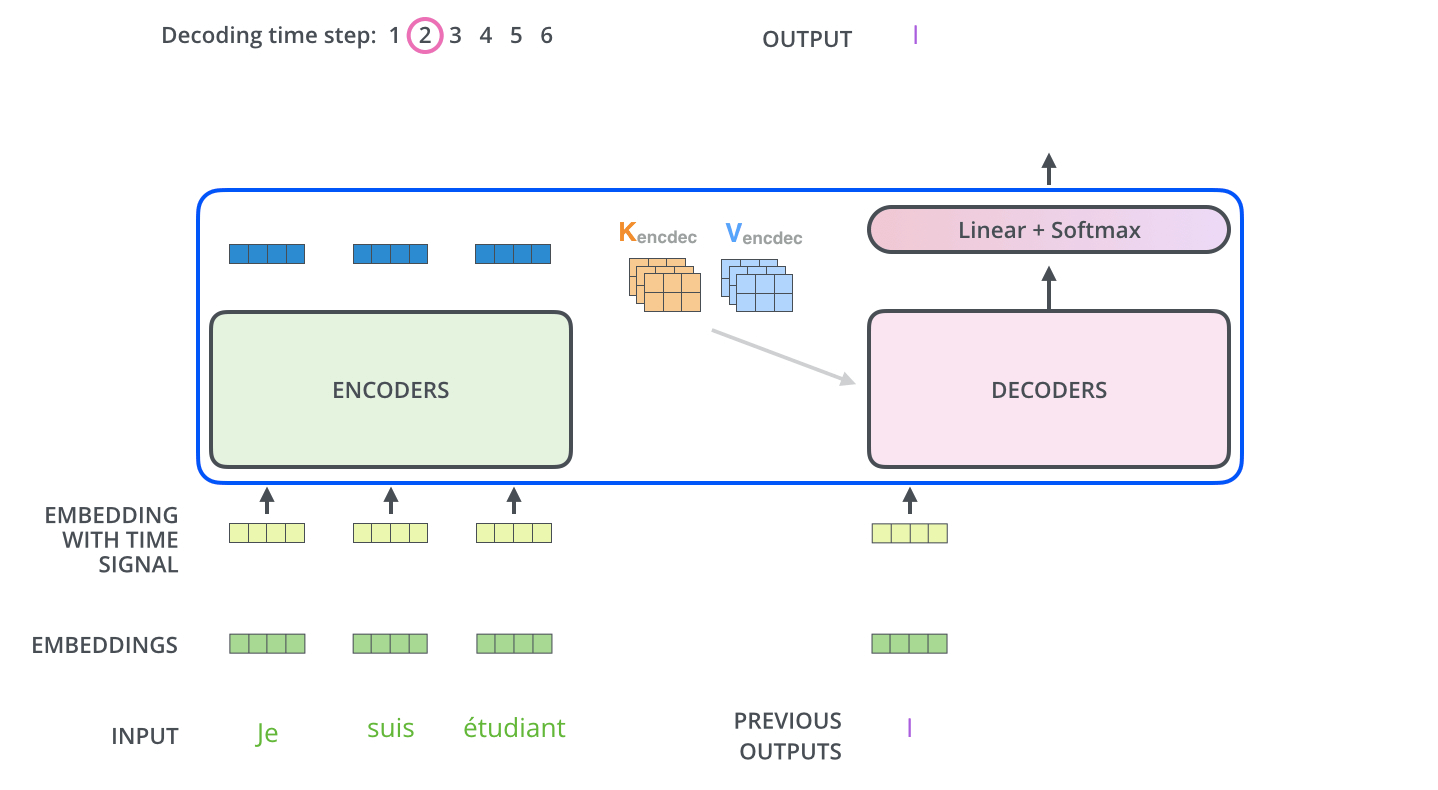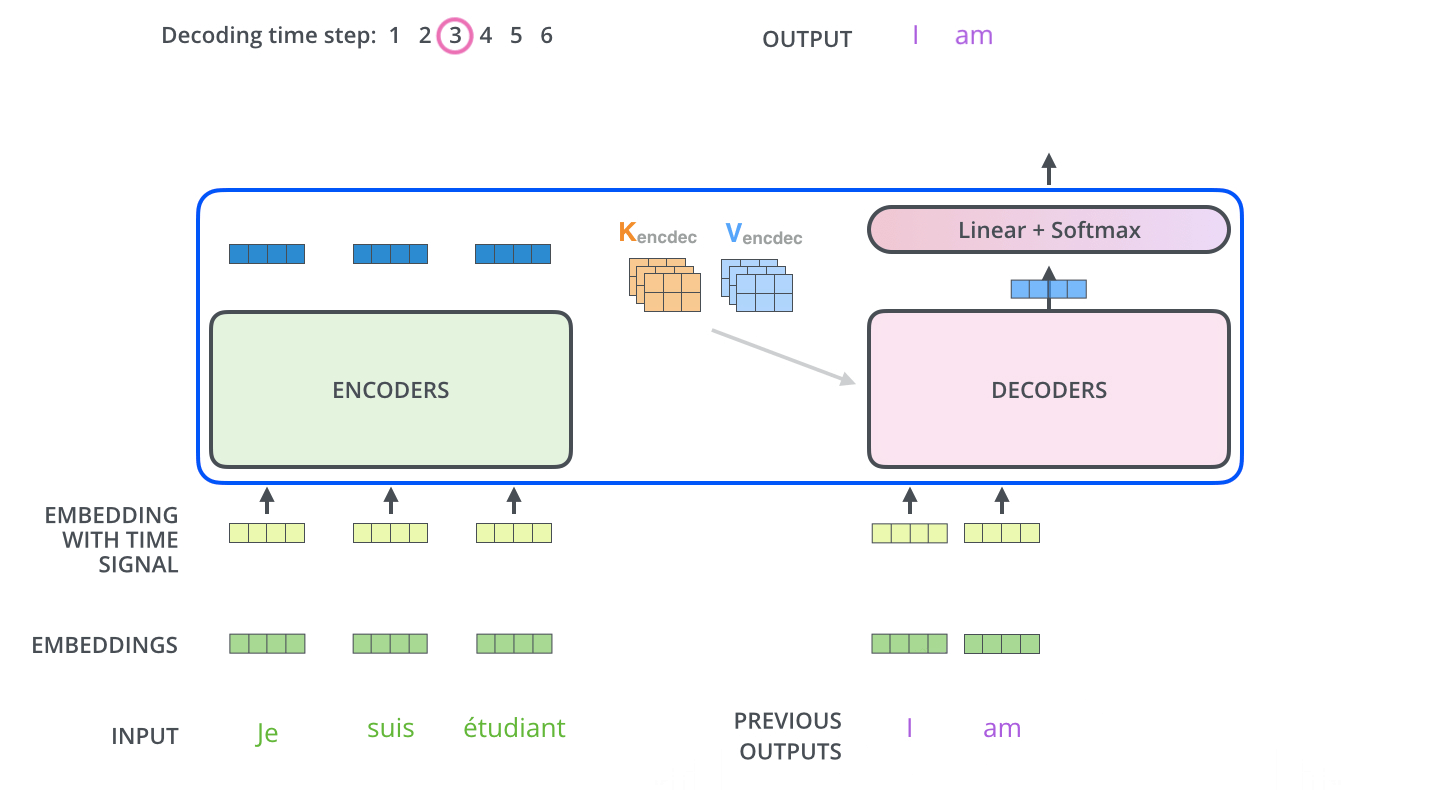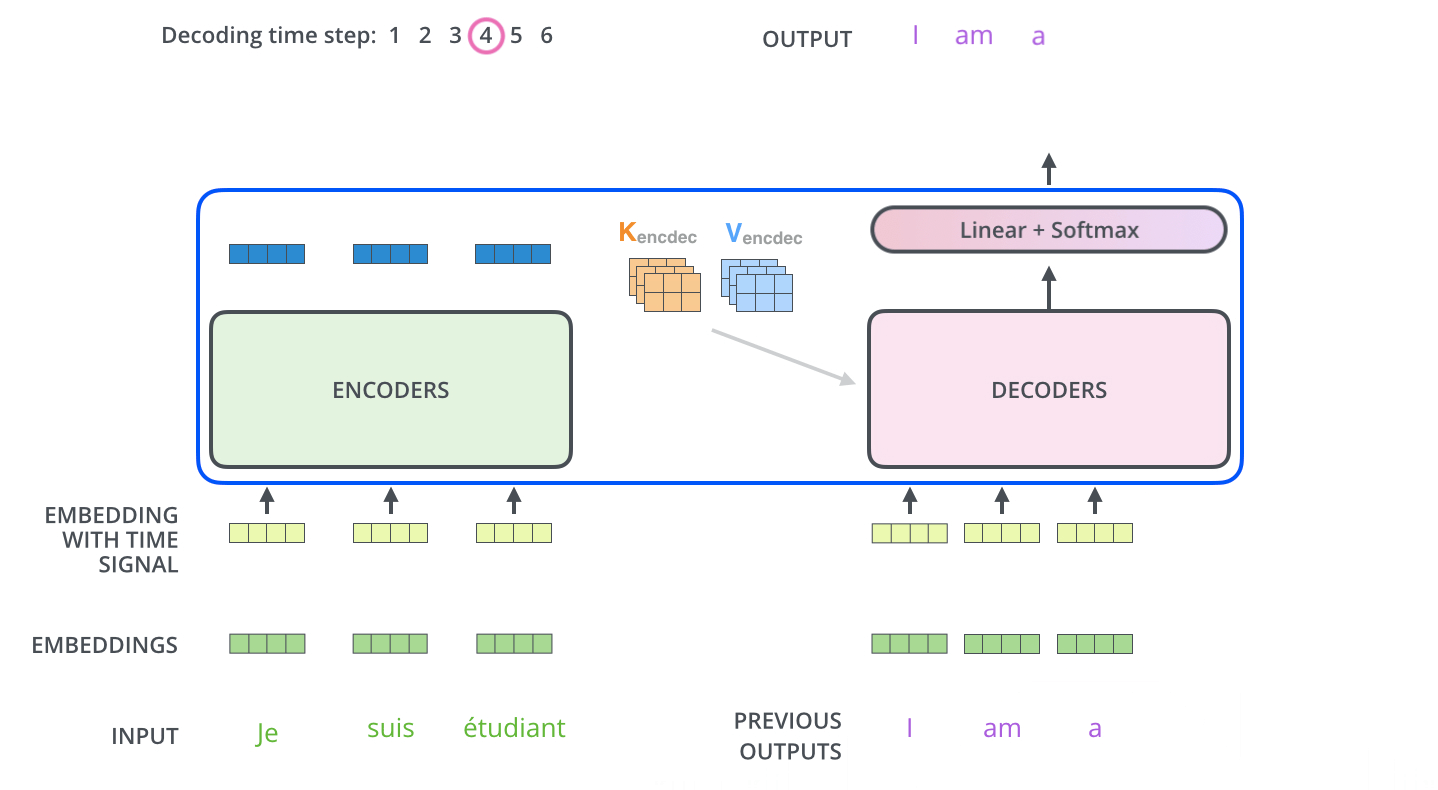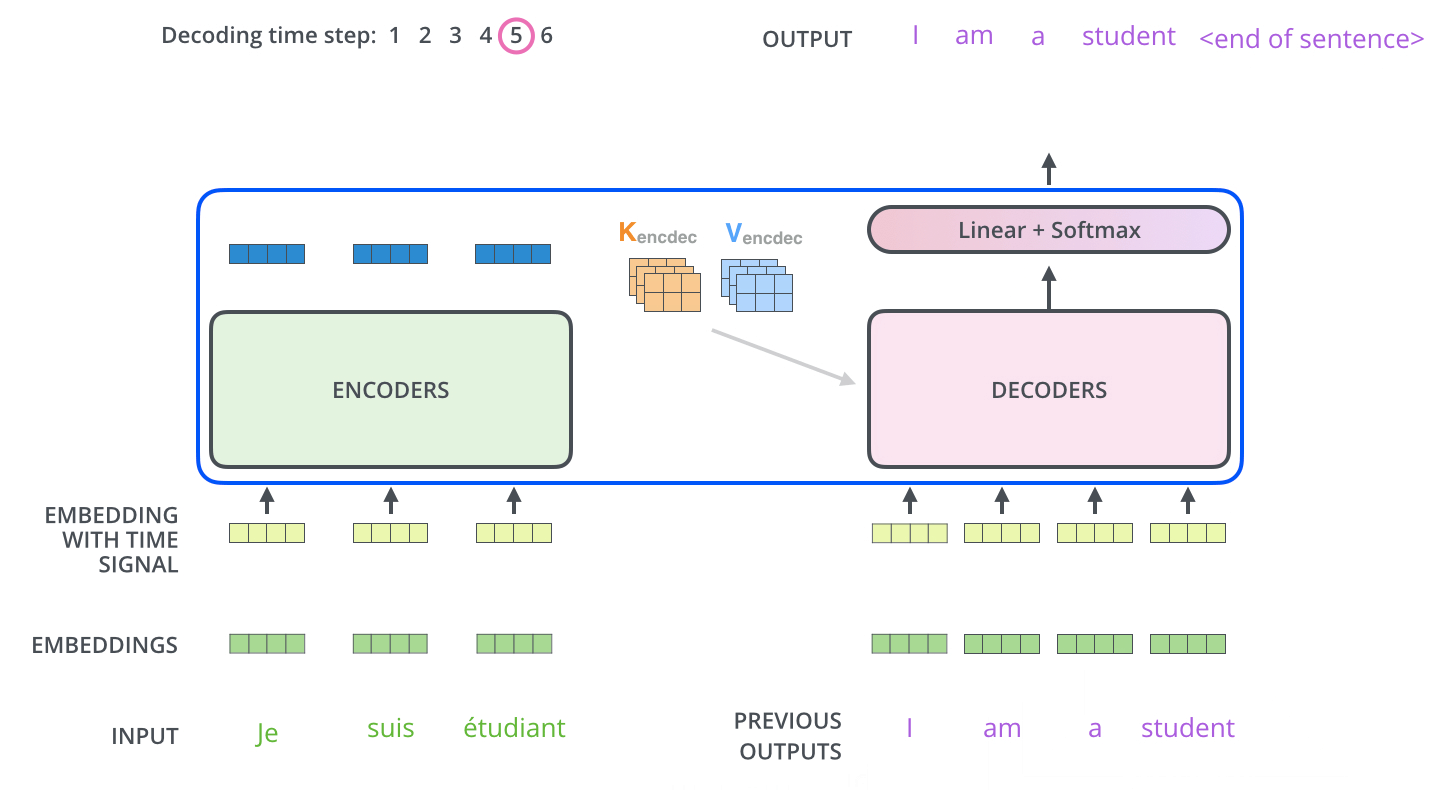
Decoder 내에 있는 Self-Attention layer들은 Encoder와는 조금 다르게 작동합니다.
Decoder에서의 Self-Attention layer는 ouput sequence 내에서 현재 위치의 이전 단어들에 대해서만 attend(참석) 가능합니다. 이것은 Self-Attention 계산 과정에서 Softmax를 취하기 전에 현재 step 이후의 위치들에 대해서 Masking(-inf 로 치환) 함으로써 가능해집니다.
"Encoder-Decoder Attention" layer는 Multi-Headed Self-Attention과 한 가지를 제외하고는 똑같은 방법으로 작동합니다.
그 한가지는 Qeury 행렬들을 그 밑의 Layer에서 가져오고 Key와 Value 행렬들은 Encoder의 출력에서 가져온다는 점입니다.
마지막 Linear Layer와 Softmax Layer
여러 개의 Decoder를 거치고 난 후에는 소수로 이루어진 벡터 하나가 남게 됩니다. 이 하나의 벡터를 Linear layer와 Softmax를 통해 하나의 단어로 바꾸게 됩니다.
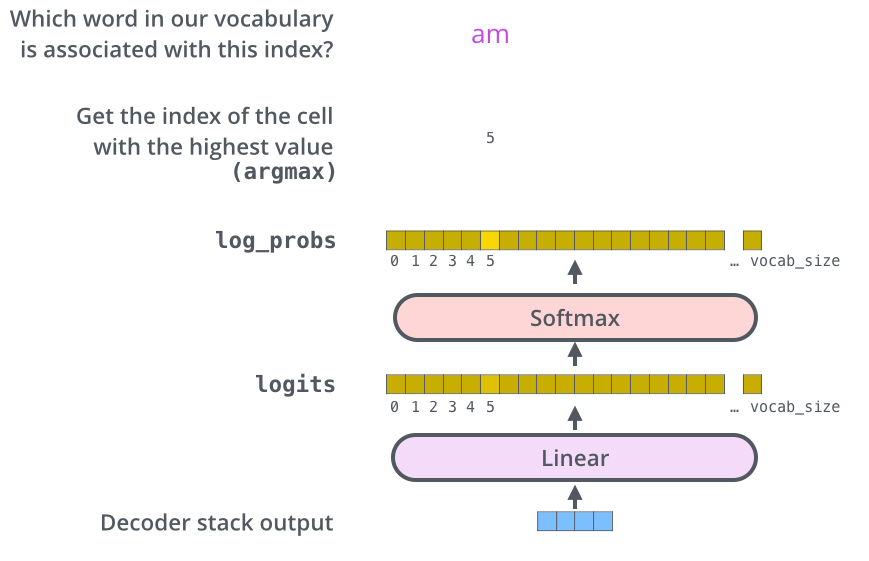
Linear layer는 Fully-Connected 신경망으로 Decoder가 마지막으로 출력한 벡터를 그보다 훨씬 더 큰 사이즈의 벡터인 logits 벡터로 투영시킵니다.
모델이 Training 데이터에서 총 10,000개의 영어 단어를 학습하였다고 가정(모델의 "output vocabulary")한다면, 이 경우에 logits vector의 크기는 10,000이 될 것입니다.(벡터의 각 셀은 그에 대응하는 각 단어에 대한 점수가 된다. 이는 Linear layer의 결과로서 나오는 출력에 대해서 해석을 할 수 있다는 뜻.)
그 다음에 나오는 Softmax layer는 이 점수들을 확률로 변환해주는 역할을 합니다. 셀들의 변환된 확률 값들은 모두 양수 값을 가지며 다 더하면 1이 됩니다. 가장 높은 확률 값을 가지는 셀에 해당하는 단어가 해당 step의 최종 결과물로 출력되게 됩니다.
'Paper Review' 카테고리의 다른 글
| [DeConvNet] Learning Deconvolution Network for Semantic Segmentation (0) | 2023.06.08 |
|---|---|
| [FCN] Fully Convolutional Networks for Semantic Segmentation (0) | 2023.03.31 |
| [Transformer] Attention Is All You Need (1) (0) | 2023.03.23 |
| [R-CNN] Rich feature hierarchies for accurate object detection and semantic segmentation 정리 (2) | 2023.03.16 |
| [ResNet] Deep Residual Learning for Image Recongnition (0) | 2022.08.03 |
Attention Is All You Need
해당 글과 그림의 출처는 lllustrated Transformer과 lllustrated Transformer(번역)을 참고하였습니다.
Positional Encoding을 이용해서 Sequence(시퀀스)의 순서 나타내기
RNN이 자연어 처리에서 유용했던 이유는 단어의 위치에 따라 단어를 순차적으로 입력받아서 처리하는 RNN의 특성으로 인해 각 단어의 위치 정보(Position Information)를 가질 수 있다는 점에 있었습니다.
하지만 Transformer 모델에서는 입력 문장에서 단어들의 순서에 대해서 고려하고 있지 않으므로 단어의 위치 정보를 다른 방식으로 알려줄 필요가 있습니다.
이를 위해서, Transformer 모델은 각각의 입력 embedding에 "positional encoding"이라고 불리는 하나의 벡터를 추가합니다. 이 벡터들은 모델이 학습하는 특정한 패턴을 따르는데, 이러한 패턴은 모델이 각 단어의 위치와 시퀀스 내의 다른 단어 간의 위치 차이에 대한 정보를 알 수 있게 해줍니다. 이 벡터들을 추가하기로 한 배경에는 이 값들을 단어에 embedding에 추가하는 것이 나중에 query/key/value 벡터들로 투영되었을 때 단어들 간의 거리를 늘릴 수 있다는 점 때문입니다.

모델에게 단어의 순서에 대한 정보를 주기 위하여, 위치 별로 특정한 패턴을 따르는 positional encoding 벡터들을 추가합니다.
만약 embedding의 사이즈가 4라고 가정한다면, 실제로 각 위치에 따른 positional encoding은 다음과 같은 것입니다.

positional encoding 값들은 다음 두 개의 함수를 사용해서 구합니다.
$$ PE(pos, 2i) = sin(pos/10000^{2i/d_{model}}) $$
$$ PE(pos, 2i+1) = cos(pos/10000^{wi/d_{model}})$$
\(sin\)함수와 \(cos\)함수의 그래프를 상기해보면 요동치는 값의 형태를 생각할 수 있는데, transformer는 이 값들을 임베딩 벡터에 더해주므로서 단어의 순서 정보를 더하여 줍니다.

위 함수 식에서 \(pos\)는 입력 문장에서의 임베딩 벡터의 위치를 나타내며, \(i\)는 임베딩 벡터 내의 차원의 인덱스를 의미합니다. (임베딩 벡터 내의 각 차원의 인덱스가 짝수면 \(sin\), 홀수면 \(cos\) 함수의 값 사용)
위와 같은 positional encoding 방법을 사용하면 순서 정보가 보존되는데, 예를 들어 각 임베딩 벡터에 positional encoding 값을 더하면 같은 단어라고 하더라도 문장 내의 위치에 따라서 transformer의 입력으로 들어가는 임베딩 벡터의 값이 달라집니다.
다음 그림에서 각 행은 하나의 벡터에 대한 positional encoding에 해당합니다. 그러므로 첫 번째 행은 우리가 입력 문장의 첫 번째 단어의 embedding 벡터에 더할 positional encoding 벡터입니다.
각 행은 512개의 셀을 가진 벡터이며 각 셀의 값은 -1과 1 사이를 가집니다. 다음 그림은 이 셀들의 값들에 대해 색깔을 다르게 나타내어 positional encoding 벡터들이 가지는 패턴을 볼 수 있도록 시각화 하였습니다.


20개의 단어와 그의 크기 512인 embedding에 대한 positional encoding의 실제 예시입니다. 위 그림에서 볼 수 있듯이 이 벡터들은 중간 부분이 반으로 나눠져 있습니다. 그 이유는 바로 왼쪽 반은(256) \(sin\) 함수에 의해서 생성되었고, 나머지 오른쪽 반은 또 다른 함수인 \(cos\) 함수에 의해 생성되었기 때문입니다. 그 후 이 두값은 연결되어 하나의 positional encoding 벡터를 이루고 있습니다.
본 논문에서 이러한 방법은 본 적이 없는 길이의 시퀀스에 대해서도 positional encoding을 생성할 수 있기 때문에 scalability에서 큰 이점을 가진다고 합니다. (예를 들어, 이미 학습된 모델이 자신의 학습 데이터보다도 더 긴 문장에 대해서 번역을 해야 할 때에도 \(sin\)과 \(cos\)으로 이루어진 식은 positional encoding을 생성해낼 수 있습니다.)
The Residuals
Encoder를 넘어가기 전 한 가지를 더 짚자면, 각 encoder 내의 sub-layer가 residual connection으로 연결되어 있으며, 그 후에는 layer-normalization 과정을 거친다는 것입니다.

이 벡터들과 layer-normalization 과정을 시각화 한다면 다음과 같습니다.

이것은 decoder 내에 있는 sub-layer 들에도 똑같이 적용되어 있습니다. 만약 2개의 encoder와 decoder로 이루어진 단순한 Transformer를 생각한다면 다음과 같습니다.

The Decoder Side
Encoder에서 사용되는 대부분의 개념들이 Decoder에도 사용됩니다.
먼저 transformer에서 사용되는 3가지의 Attention에 대해서 간단히 정리해보겠습니다.


첫 번째 그림인 Self-Attention은 Encoder에서 이루어지지만, 두 번째 그림인 Self-Attention과 세 번째 그림인 Encoder-Decoder Attention은 Decoder에서 이루어집니다. Self-Attention은 본질적으로 Query, Key, Value가 동일한 경우를 말합니다.(벡터의 값이 같은게 아니라, 벡터의 출처가 같다는 의미입니다.) 반면, Encoder-Decoder Attention에서는 Qeury가 Decoder의 벡터인 반면에 Key와 Value가 Encoder의 벡터이므로 Self-Attention이라고 부르지 않습니다.
Encoder의 Self-Attention : Query = Key = Value
Decoder의 Masked-Self-Attention : Query = Key = Value
Decoder의 Encdoer-Decoder Attention : Query - Decoder 벡터 / Key = Value - Encoder 벡터
먼저 Encoder가 입력 시퀀스를 처리하기 시작합니다. 그 다음 가장 윗단의 Encoder의 출력은 Attention 벡터들인 \(K\)와 \(V\)로 변형됩니다. 이 \(K\), \(V\) 벡터들은 이제 각 Decoder의 "Encoder-Decoder Attention" layer 에서 Decoder가 입력 시퀀스에서 적절한 장소에 집중할 수 있도록 도와줍니다.

이 단계가 끝나면 Decoding 단계가 시작됩니다. Decoding 단계의 각 step은 출력 시퀀스의 한 element를 출력합니다.
Decoding step은 Decoder가 출력을 완료 했다는 Special 기호인 <End of Sentence>를 출력할 때까지 반복됩니다. 각 setp 마다 출력된 단어는 다음 step의 가장 밑단의 Decoder에 들어가고 Encoder와 마찬가지로 여러 개의 Decoder를 거쳐 올라갑니다. Encoder의 입력에 했던 것과 동일하게 embedding 후, postional encoding을 추가하여 Decoder에게 각 단어의 우치 정보를 더해줍니다.

Decoder 내에 있는 Self-Attention layer들은 Encoder와는 조금 다르게 작동합니다.
Decoder에서의 Self-Attention layer는 ouput sequence 내에서 현재 위치의 이전 단어들에 대해서만 attend(참석) 가능합니다. 이것은 Self-Attention 계산 과정에서 Softmax를 취하기 전에 현재 step 이후의 위치들에 대해서 Masking(-inf 로 치환) 함으로써 가능해집니다.
"Encoder-Decoder Attention" layer는 Multi-Headed Self-Attention과 한 가지를 제외하고는 똑같은 방법으로 작동합니다.
그 한가지는 Qeury 행렬들을 그 밑의 Layer에서 가져오고 Key와 Value 행렬들은 Encoder의 출력에서 가져온다는 점입니다.
마지막 Linear Layer와 Softmax Layer
여러 개의 Decoder를 거치고 난 후에는 소수로 이루어진 벡터 하나가 남게 됩니다. 이 하나의 벡터를 Linear layer와 Softmax를 통해 하나의 단어로 바꾸게 됩니다.
Linear layer는 Fully-Connected 신경망으로 Decoder가 마지막으로 출력한 벡터를 그보다 훨씬 더 큰 사이즈의 벡터인 logits 벡터로 투영시킵니다.
모델이 Training 데이터에서 총 10,000개의 영어 단어를 학습하였다고 가정(모델의 "output vocabulary")한다면, 이 경우에 logits vector의 크기는 10,000이 될 것입니다.(벡터의 각 셀은 그에 대응하는 각 단어에 대한 점수가 된다. 이는 Linear layer의 결과로서 나오는 출력에 대해서 해석을 할 수 있다는 뜻.)
그 다음에 나오는 Softmax layer는 이 점수들을 확률로 변환해주는 역할을 합니다. 셀들의 변환된 확률 값들은 모두 양수 값을 가지며 다 더하면 1이 됩니다. 가장 높은 확률 값을 가지는 셀에 해당하는 단어가 해당 step의 최종 결과물로 출력되게 됩니다.

'Paper Review' 카테고리의 다른 글
| [DeConvNet] Learning Deconvolution Network for Semantic Segmentation (0) | 2023.06.08 |
|---|---|
| [FCN] Fully Convolutional Networks for Semantic Segmentation (0) | 2023.03.31 |
| [Transformer] Attention Is All You Need (1) (0) | 2023.03.23 |
| [R-CNN] Rich feature hierarchies for accurate object detection and semantic segmentation 정리 (2) | 2023.03.16 |
| [ResNet] Deep Residual Learning for Image Recongnition (0) | 2022.08.03 |
