EfficientNet
Abstract
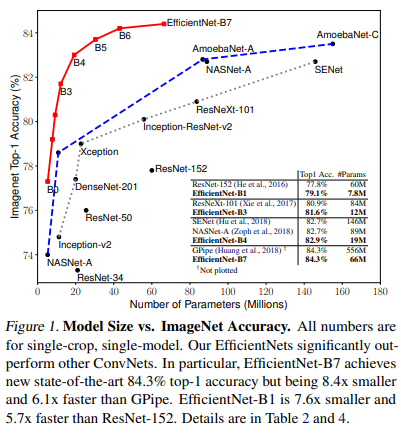
이 논문에서는 네트워크의 깊이(Depth), 너비(Width), 이미지의 해상도(Resolution)을 "균형있게" 조절(Scaling)하면 성능이 향상된다는 것을 파악했습니다.깊이, 너비, 해상도를 compound coefficient를 사용하여 균일하게 확장하는 새로운 스케일링 방법을 제시하였고, 이를 사용하여 훨씬 적은 파라미터로 뛰어난 정확도와 효율성을 달성하였습니다.
Introduction
기존의 Convolution Network들은 일반적으로 깊이, 너비, 이미지의 해상도 중 하나만 스케일링하여 성능을 개선했습니다.
논문의 저자는 네트워크의 너비, 깊이, 이미지의 해상도를 균형있게 일정한 비율로 조정한다면 높은 성능을 낼 수 있다는 것을 파악했습니다. 따라서, 이 세가지의 요소를 균형있게 조정할 수 있는 Compound Scaling Method을 제안합니다.
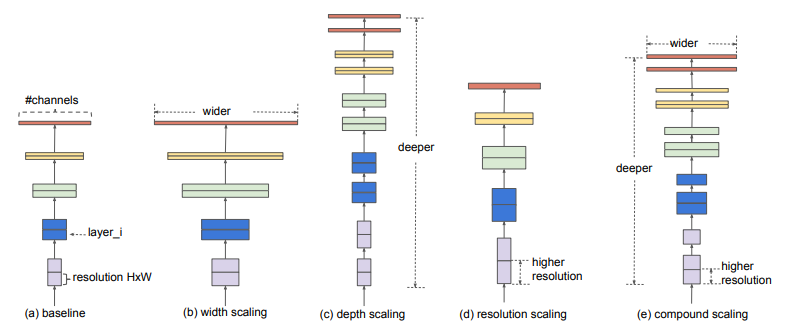
Compund Scaling Method는 네트워크의 너비, 깊이, 해상도를 고정된 상수비로 균일하게 확장하여 최적의 값을 Grid Search를 통해 찾습니다.
계산 리소스가 \(2^N\)배 큰 모델을 디자인하고 싶다면, 깊이는 \(\alpha ^ N\) 너비는 \(\beta ^ N\) 해상도는 \(\gamma ^ N\) 배로 증가시켜 찾습니다.
Compound Model Scaling
Problem Formulation
$$ Y = F_i ( X_i ) $$
\(Y\) : output tensor, \(F\) : operator, \(X\) : input tensor <\(H_i, W_i, C_i\)>,
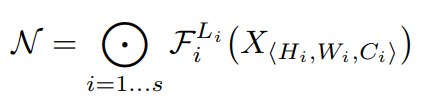
딥러닝 모델(ex. ConvNet)은 위 수식과 같이 정의할 수 있습니다. 이 모델을 개선하기 위해서는 다양한 방법이 있는데, 가장 대표적인 방법은 새로운 Architecture \(F\)를 찾는 것입니다.(ex. Inception, VGGNet, ResNet)
이와는 다르게 \(F\)는 고정한 채로 최적의 Scale을 연구하는 방법을 이 논문에서 사용합니다.

위 수식과 같이 성능(Accuracy)를 최대로 하는 Depth, Width, Resolution 변수를 찾는 것 입니다.
Scaling Dimensions
가장 중요한 문제는 최적의 d, w, r은 서로 연관되어 있다는 것이고 다른 제약조건에서 값이 변한다는 것입니다.
그래서 이 중 하나로만 scaling 하는 방법이 많이 제시되었습니다.
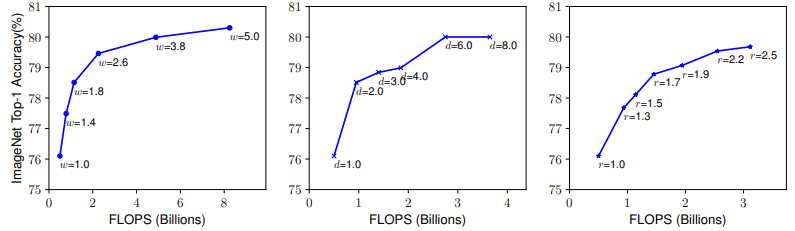
\(\rightarrow\) width, depth, resolution 모두 dimention을 scale up 하여도 클 수록 성장 폭이 낮아짐
Depth (d)
- 가장 일반적으로 사용하는 scaling 기법
- 풍부하고 복잡한 특징을 잘 잡아내고 일반화가 잘 되지만, 깊은 모델에서는 grandient vanishing 문제로 학습이 어려움
- skip connection, batch normalization 방법이 있지만 매우 깊은 모델에서는 효과가 없음 (ResNet에서 확인)
Width (w)
- 주로 작은 모델에서 사용하는 scaling 기법
- wider 할 수록 학습 과정에서 세밀한 특징을 잘 잡아내는 경향이 있음 (채널 수가 증가하기 때문에 당연하다고 생각)
- 하지만 극단적으로 넓지만 얕은 모델은 더 높은 수준의 특징을 포착하기 어려움 (특징 적인 부분이 제한 적이기 때문이라고 생각)
Resolution (r)
- 고해상도 이미지일 수록 세밀한 패턴을 잘 잡아냄
- 어느 순간부터는 Accuracy의 큰 상승 없이 FLOPS만 늘어날 수 있음
Compound Scaling
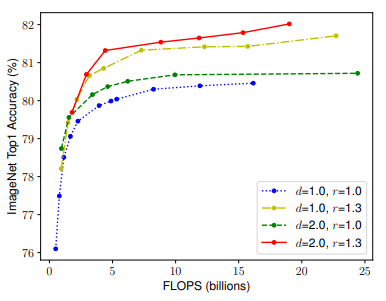
직관적으로, 더 높은 해상도의 이미지에 대해서는 네트워크를 깊게 만들어 더 넓은 영역에 있는 특징 (receptive fields)를 더 잘 잡아낼 수 있도록 하는 것이 유리합니다다. 즉, 더 큰 이미지(resolution)일 수록 특징(width)도 많이 담고 있고, 이를 잡아내기 위해서는 깊이(Depth)를 증가시킬 필요가 있습니다.
이 세가지 변수는 밀접하게 연관되어 있어, 이를 같이 조절하는 것이 도움이 될 수 있을 것이라 판단 했습니다..
Depth에서 Convolution Layer가 \(\alpha\)배 늘어나면 FLOPS도 \(\alpha\)배가 늘어남.
Width에서 Channel이 \(\beta\)배 늘어나면 FLOPOS는 \(\beta^2)배 늘어남
Resolution에서 W, H가 \(\gamma\)배 늘어나면 FLOPS는 \(\gamma^2\)배 늘어남
결과적으로 FLOPS는 Depth, Width^2, Resolution^2에 비례한다고 할 수 있습니다.

EfficientNet Architecture
앞선 조건에서 \(F\)는 바뀌지 않아야 하기 때문에 처음부터 좋은 baseline network를 논문 저자는 EfficientNet으로 정했습니다.
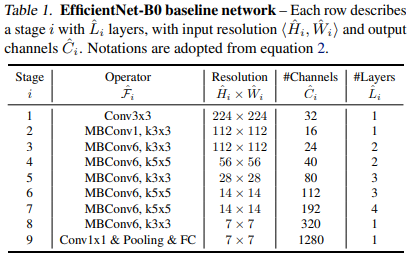
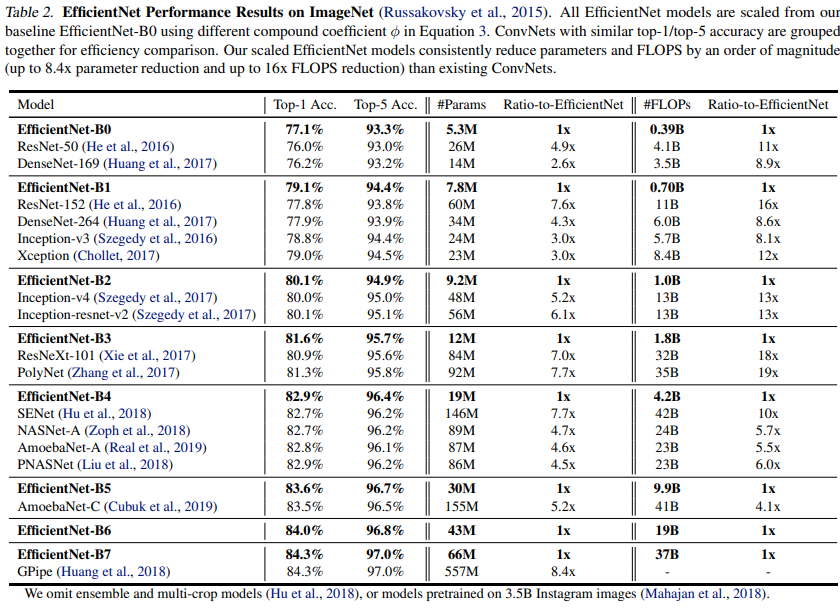
EfficientNet은 Neural Architectrue Search(NAS) 방법을 사용하여 찾았습니다. 즉, 딥러닝을 사용하여 딥러닝 모델을 찾는 것입니다.
다음으로 적절한 d, w, r을 찾아야 하는데 \(\alpha\), \(\beta\), \(\gamma\)를 찾아 큰 모델에 적용하면 더 좋은 성능을 내겠지만, 찾는 비용이 더 많이 들었습니다.
따라서 논문 저자는 각각의 조합을 Small Grid Search로 찾았고 결과, \(\alpha\) = 1.2, \(\beta\) = 1.1, \(\gamma\) = 1.5 일 때 성능과 연산량을 고려한 성능이 가장 높았습니다.
이렇게 나온 네트워크를 EfficientNet-B0라고 합니다.
여기서 더 큰 EfficientNet을 만드는 방법은 비율을 고정한 채로 Scale만 키워주면 됩니다.
구현
EfficientNet을 구성하는 핵심 모듈인 MBConv Block입니다.
(이는 MobileNetv2에서 제안된 블럭입니다.)
import torch
import torch.nn as nn
import torch.nn.functional as F
class MBConvBlock(nn.Module):
def __init__(self, in_channels, out_channels, kernel_size, stride, expand_ratio):
super(MBConvBlock, self).__init__()
hidden_dim = in_channels * expand_ratio
self.expand = in_channels != out_channels
self.block = nn.Sequential(
# Pointwise Convolution
nn.Conv2d(in_channels, hidden_dim, 1, 1, 0, bias=False),
nn.BatchNorm2d(hidden_dim),
nn.ReLU6(inplace=True),
# Depthwise Convolution
nn.Conv2d(hidden_dim, hidden_dim, kernel_size, stride, kernel_size//2, groups=hidden_dim, bias=False),
nn.BatchNorm2d(hidden_dim),
nn.ReLU6(inplace=True),
# Pointwise Convolution Linear
nn.Conv2d(hidden_dim, out_channels, 1, 1, 0, bias=False),
nn.BatchNorm2d(out_channels),
)
def forward(self, x):
if self.expand:
return self.block(x)
else:
return x + self.block(x)다음은 EfficientNet입니다. B0의 구성에 맞게 설계하였습니다.
class EfficientNet(nn.Module):
def __init__(self):
super(EfficientNet, self).__init__()
self.stem = nn.Sequential(
nn.Conv2d(3, 32, 3, 2, 1, bias=False),
nn.BatchNorm2d(32),
nn.ReLU6(inplace=True)
)
self.blocks = nn.Sequential(
MBConvBlock(32, 16, 3, 1, 1),
MBConvBlock(16, 24, 3, 2, 6),
MBConvBlock(24, 40, 5, 2, 6),
MBConvBlock(40, 80, 3, 2, 6),
MBConvBlock(80, 112, 5, 1, 6),
MBConvBlock(112, 192, 5, 2, 6),
MBConvBlock(192, 320, 3, 1, 6)
)
self.head = nn.Sequential(
nn.Conv2d(320, 1280, 1, 1, 0, bias=False),
nn.BatchNorm2d(1280),
nn.ReLU6(inplace=True),
nn.AdaptiveAvgPool2d(1),
nn.Flatten(),
nn.Linear(1280, 1000)
)
def forward(self, x):
x = self.stem(x)
x = self.blocks(x)
x = self.head(x)
return x
참고
[1] https://arxiv.org/pdf/1905.11946
[2] https://ffighting.net/deep-learning-paper-review/vision-model/efficientnet/
'Paper Review' 카테고리의 다른 글
EfficientNet
Abstract

이 논문에서는 네트워크의 깊이(Depth), 너비(Width), 이미지의 해상도(Resolution)을 "균형있게" 조절(Scaling)하면 성능이 향상된다는 것을 파악했습니다.깊이, 너비, 해상도를 compound coefficient를 사용하여 균일하게 확장하는 새로운 스케일링 방법을 제시하였고, 이를 사용하여 훨씬 적은 파라미터로 뛰어난 정확도와 효율성을 달성하였습니다.
Introduction
기존의 Convolution Network들은 일반적으로 깊이, 너비, 이미지의 해상도 중 하나만 스케일링하여 성능을 개선했습니다.
논문의 저자는 네트워크의 너비, 깊이, 이미지의 해상도를 균형있게 일정한 비율로 조정한다면 높은 성능을 낼 수 있다는 것을 파악했습니다. 따라서, 이 세가지의 요소를 균형있게 조정할 수 있는 Compound Scaling Method을 제안합니다.

Compund Scaling Method는 네트워크의 너비, 깊이, 해상도를 고정된 상수비로 균일하게 확장하여 최적의 값을 Grid Search를 통해 찾습니다.
계산 리소스가 \(2^N\)배 큰 모델을 디자인하고 싶다면, 깊이는 \(\alpha ^ N\) 너비는 \(\beta ^ N\) 해상도는 \(\gamma ^ N\) 배로 증가시켜 찾습니다.
Compound Model Scaling
Problem Formulation
$$ Y = F_i ( X_i ) $$
\(Y\) : output tensor, \(F\) : operator, \(X\) : input tensor <\(H_i, W_i, C_i\)>,
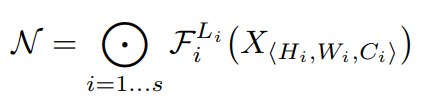
딥러닝 모델(ex. ConvNet)은 위 수식과 같이 정의할 수 있습니다. 이 모델을 개선하기 위해서는 다양한 방법이 있는데, 가장 대표적인 방법은 새로운 Architecture \(F\)를 찾는 것입니다.(ex. Inception, VGGNet, ResNet)
이와는 다르게 \(F\)는 고정한 채로 최적의 Scale을 연구하는 방법을 이 논문에서 사용합니다.

위 수식과 같이 성능(Accuracy)를 최대로 하는 Depth, Width, Resolution 변수를 찾는 것 입니다.
Scaling Dimensions
가장 중요한 문제는 최적의 d, w, r은 서로 연관되어 있다는 것이고 다른 제약조건에서 값이 변한다는 것입니다.
그래서 이 중 하나로만 scaling 하는 방법이 많이 제시되었습니다.

\(\rightarrow\) width, depth, resolution 모두 dimention을 scale up 하여도 클 수록 성장 폭이 낮아짐
Depth (d)
- 가장 일반적으로 사용하는 scaling 기법
- 풍부하고 복잡한 특징을 잘 잡아내고 일반화가 잘 되지만, 깊은 모델에서는 grandient vanishing 문제로 학습이 어려움
- skip connection, batch normalization 방법이 있지만 매우 깊은 모델에서는 효과가 없음 (ResNet에서 확인)
Width (w)
- 주로 작은 모델에서 사용하는 scaling 기법
- wider 할 수록 학습 과정에서 세밀한 특징을 잘 잡아내는 경향이 있음 (채널 수가 증가하기 때문에 당연하다고 생각)
- 하지만 극단적으로 넓지만 얕은 모델은 더 높은 수준의 특징을 포착하기 어려움 (특징 적인 부분이 제한 적이기 때문이라고 생각)
Resolution (r)
- 고해상도 이미지일 수록 세밀한 패턴을 잘 잡아냄
- 어느 순간부터는 Accuracy의 큰 상승 없이 FLOPS만 늘어날 수 있음
Compound Scaling

직관적으로, 더 높은 해상도의 이미지에 대해서는 네트워크를 깊게 만들어 더 넓은 영역에 있는 특징 (receptive fields)를 더 잘 잡아낼 수 있도록 하는 것이 유리합니다다. 즉, 더 큰 이미지(resolution)일 수록 특징(width)도 많이 담고 있고, 이를 잡아내기 위해서는 깊이(Depth)를 증가시킬 필요가 있습니다.
이 세가지 변수는 밀접하게 연관되어 있어, 이를 같이 조절하는 것이 도움이 될 수 있을 것이라 판단 했습니다..
Depth에서 Convolution Layer가 \(\alpha\)배 늘어나면 FLOPS도 \(\alpha\)배가 늘어남.
Width에서 Channel이 \(\beta\)배 늘어나면 FLOPOS는 \(\beta^2)배 늘어남
Resolution에서 W, H가 \(\gamma\)배 늘어나면 FLOPS는 \(\gamma^2\)배 늘어남
결과적으로 FLOPS는 Depth, Width^2, Resolution^2에 비례한다고 할 수 있습니다.

EfficientNet Architecture
앞선 조건에서 \(F\)는 바뀌지 않아야 하기 때문에 처음부터 좋은 baseline network를 논문 저자는 EfficientNet으로 정했습니다.

EfficientNet은 Neural Architectrue Search(NAS) 방법을 사용하여 찾았습니다. 즉, 딥러닝을 사용하여 딥러닝 모델을 찾는 것입니다.
다음으로 적절한 d, w, r을 찾아야 하는데 \(\alpha\), \(\beta\), \(\gamma\)를 찾아 큰 모델에 적용하면 더 좋은 성능을 내겠지만, 찾는 비용이 더 많이 들었습니다.
따라서 논문 저자는 각각의 조합을 Small Grid Search로 찾았고 결과, \(\alpha\) = 1.2, \(\beta\) = 1.1, \(\gamma\) = 1.5 일 때 성능과 연산량을 고려한 성능이 가장 높았습니다.
이렇게 나온 네트워크를 EfficientNet-B0라고 합니다.
여기서 더 큰 EfficientNet을 만드는 방법은 비율을 고정한 채로 Scale만 키워주면 됩니다.

구현
EfficientNet을 구성하는 핵심 모듈인 MBConv Block입니다.
(이는 MobileNetv2에서 제안된 블럭입니다.)
import torch
import torch.nn as nn
import torch.nn.functional as F
class MBConvBlock(nn.Module):
def __init__(self, in_channels, out_channels, kernel_size, stride, expand_ratio):
super(MBConvBlock, self).__init__()
hidden_dim = in_channels * expand_ratio
self.expand = in_channels != out_channels
self.block = nn.Sequential(
# Pointwise Convolution
nn.Conv2d(in_channels, hidden_dim, 1, 1, 0, bias=False),
nn.BatchNorm2d(hidden_dim),
nn.ReLU6(inplace=True),
# Depthwise Convolution
nn.Conv2d(hidden_dim, hidden_dim, kernel_size, stride, kernel_size//2, groups=hidden_dim, bias=False),
nn.BatchNorm2d(hidden_dim),
nn.ReLU6(inplace=True),
# Pointwise Convolution Linear
nn.Conv2d(hidden_dim, out_channels, 1, 1, 0, bias=False),
nn.BatchNorm2d(out_channels),
)
def forward(self, x):
if self.expand:
return self.block(x)
else:
return x + self.block(x)
다음은 EfficientNet입니다. B0의 구성에 맞게 설계하였습니다.
class EfficientNet(nn.Module):
def __init__(self):
super(EfficientNet, self).__init__()
self.stem = nn.Sequential(
nn.Conv2d(3, 32, 3, 2, 1, bias=False),
nn.BatchNorm2d(32),
nn.ReLU6(inplace=True)
)
self.blocks = nn.Sequential(
MBConvBlock(32, 16, 3, 1, 1),
MBConvBlock(16, 24, 3, 2, 6),
MBConvBlock(24, 40, 5, 2, 6),
MBConvBlock(40, 80, 3, 2, 6),
MBConvBlock(80, 112, 5, 1, 6),
MBConvBlock(112, 192, 5, 2, 6),
MBConvBlock(192, 320, 3, 1, 6)
)
self.head = nn.Sequential(
nn.Conv2d(320, 1280, 1, 1, 0, bias=False),
nn.BatchNorm2d(1280),
nn.ReLU6(inplace=True),
nn.AdaptiveAvgPool2d(1),
nn.Flatten(),
nn.Linear(1280, 1000)
)
def forward(self, x):
x = self.stem(x)
x = self.blocks(x)
x = self.head(x)
return x
참고
[1] https://arxiv.org/pdf/1905.11946
[2] https://ffighting.net/deep-learning-paper-review/vision-model/efficientnet/
