MobileNet
MobileNet은 경량화에 집중하였습니다. 그 이유는 핸드폰이나 임베디드 시스템 같이 저용량 메모리환경에서 딥러닝을 사용하기 위해서입니다. MobileNet의 경량화 비결을 알기 위해선 Depthwise Separable Convolusion의 이해가 필요합니다.
Architecture
Depthwise Separable Convolution
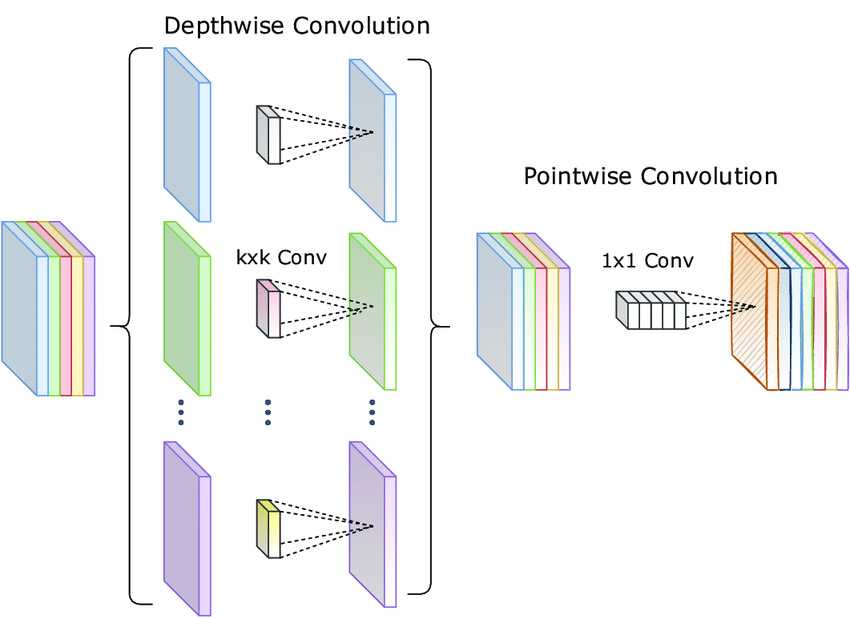
Depthwise Separable Convolution은 위 그림과 같이 Depthwise Convolution과 Pointwise Convolution의 두 개의 별도 단계로 분리하여 계산 효율성을 크게 향상시키는 기법입니다.
Standard Convolution
$$ D_K \cdot D_K \cdot M \cdot M \cdot D_F \cdot D_F $$
\(D_K\) : 입력값 크기(W, H), \(M\) : 입력 채널 수, \(M\) : 출력 채널 수, \(D_F\) : 출력값 크기(W, H)
Depthwise Convolution
Depthwise Convolution의 경우 각 입력 채널에 대하여 3x3 Conv 하나의 필터가 연산을 수행하여 하나의 피쳐맵을 생성합니다. 입력 채널 수가 M개이면 M개의 피쳐맵을 생성합니다 (출력 채널 수 == 입력 채널 수). 각 채널마다 독립적으로 연산을 수행하여 Spatial Correlation을 계산하는 것입니다.
$$ D_K \cdot D_K \cdot M \cdot D_F \cdot D_F $$
\(D_K\) : 입력값 크기(W, H) , \(M\) : 입력 채널 수, \(D_F\) : 출력값 크기(W, H)
Pointwise Convolution
Potinwise Convolution은 Depthwise Convolution이 생성한 피쳐맵들을 1x1 Conv로 채널 수를 조정하는 작업을 말합니다.
1x1 Conv는 모든 채널에 대해 연산을 수행하므로, Cross Channel Correlation을 계산하게 되는 것입니다. 즉, 채널 간은 정보를 결합하고, 원하는 출력 채널 수로 조정할 수 있습니다.
$$ M \cdot N \cdot D_F \cdot D_F $$
\(M\) : 입력 채널 수, \(N\) : 출력 채널 수, \(D_F\) 출력값 크기(W, H)
연산량
$$ D_K \cdot D_K \cdot M \cdot D_F \cdot D_F + M \cdot N \cdot D_F \cdot D_F $$
Depthwise Separable Convolution의 연산량은 Depthwise Convolution의 연산량과 Poinwise Convolution 연산량의 합입니다.
이는 기존 Convolution 연산과 비교하였을 때 약 8~9배 적은 연산량을 가집니다.
Architecture
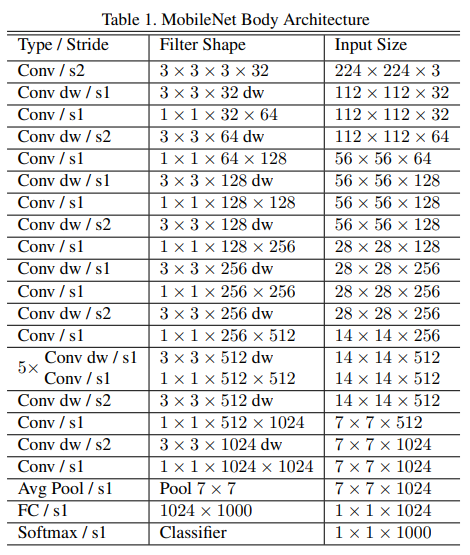
첫 번째 레이어는 Standard Conv를 사용하고 그 이후부터 Depthwise Conv와 Pointwise Conv를 번갈아가며 수행합니다.
feature map의 크기는 Stride를 2로 적용하여 크기를 절반으로 줄여주고 채널 수(필터 수)는 Ponitwise Conv를 수행할 때 지정합니다.
구현
import torch.nn as nn
class StandardConv(nn.Module):
def __init__(self, in_channels, out_channels, kernel_size, stride=1, padding=0):
super(StandardConv, self).__init__()
self.conv = nn.Conv2d(in_channels, out_channels, kernel_size, stride, padding)
def forward(self, x):
return self.conv(x)
standard_conv = StandardConv(in_channels=3, out_channels=64, kernel_size=3, padding=1)
class DepthwiseSeparableConv(nn.Module):
def __init__(self, in_channels, out_channels, kernel_size, stride=1, padding=0):
super(DepthwiseSeparableConv, self).__init__()
self.depthwise = nn.Conv2d(in_channels, in_channels, kernel_size, stride, padding, groups=in_channels)
self.pointwise = nn.Conv2d(in_channels, out_channels, 1)
def forward(self, x):
x = self.depthwise(x)
x = self.pointwise(x)
return x
depthwise_separable_conv = DepthwiseSeparableConv(in_channels=3, out_channels=64, kernel_size=3, padding=1)
Width Multiplier & Resolution Multiplier
Width Multiplier
기존의 MobileNet Architecture은 이미 작고 지연 시간이 짧지만 특정 상황에서는 더 작고 더 빠른 모델을 필요로 할 수도 있으니, Width Multiplier라고 불리는 파라미터 알파\(alpha\)를 도입합니다. 이 알파의 역할은 각 layer를 균일하게 더 얇게 만드는 것인데, input channel이 \(M\)이였다면 여기에 알파를 곱해 더 얇게 만들어줍니다.
$$ D_K \cdot D_K \cdot \alpha M \cdot D_F \cdot D_F + \alpha M \cdot \alpha N \cdot D_F \cdot D_F $$
보통 1, 0.75, 0.5, 0.25로 세팅하고 cost와 파라미터 수를 대략 알파의 거듭제곱만큼 감소시키는 효과를 가집니다.
Resolution Multiplier
Resolution Multiplier는 신경망의 계산 비용을 줄이기 위한 파라미터 \(\rho\) 입니다. \(\rho\)는 입력 이미지에 적용하여 해상도를 낮춥니다. 범위는 \(\rho \in (0,1]\)이고 네트워크 입력 해상도는 224, 192, 160, 128 입니다.
$$ D_K \cdot D_K \cdot \alpha M \cdot \rho D_F \cdot \rho D_F + \alpha M \cdot \alpha N \cdot \rho D_F \cdot \rho D_F $$
Experiments

FC를 사용한 모델과 Depthwise Separable을 사용한 MoblieNet의 결과입니다.
파라미터는 많이 감소하였으나, 정확도 부분은 약 1%만 감소했음을 확인할 수 있습니다.
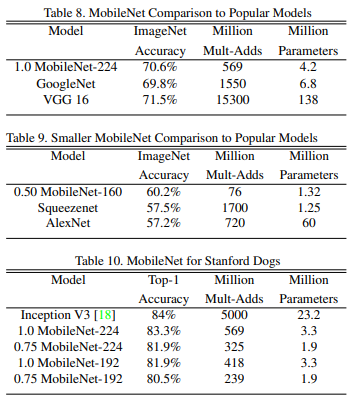
당시 사용되던 모델들과의 비교입니다. MobileNet이 VGG만큼 정확하지만 파라미터 값도 상당히 적음을 확인할 수 있습니다.
마무리
MobileNet은 정확도를 조금 내주고 더 효율적인 모델로 설계했습니다. 또한 하이퍼파라미터를 통해 다양한 환경과 요구사항에 맞춰 유연하게 조정할 수 있다는 장점을 가지고 있습니다. 고려해야할 점으로 해상도를 낮게 설정할 경우 작은 객체나 세밀한 특징을 검출하기 어려워 질 수 있겠다는 생각을 했습니다.
참고
[1] https://arxiv.org/pdf/1704.04861v1
[2] https://dacon.io/forum/406019
[3] https://velog.io/@twinjuy/MobileNet-%EB%85%BC%EB%AC%B8%EB%A6%AC%EB%B7%B0
'Paper Review' 카테고리의 다른 글
| [EfficientNet] Rethinking Model Scaling for Convolutional Neural Networks (0) | 2024.07.11 |
|---|---|
| [SENet] Squeeze and Excitation Networks (0) | 2024.07.10 |
| [GAN] Generative Adversarial Nets (0) | 2024.01.30 |
| [SegNet] A Deep ConvolutionalEncoder-Decoder Architecture for ImageSegmentation (0) | 2023.06.08 |
| [DeConvNet] Learning Deconvolution Network for Semantic Segmentation (0) | 2023.06.08 |
MobileNet
MobileNet은 경량화에 집중하였습니다. 그 이유는 핸드폰이나 임베디드 시스템 같이 저용량 메모리환경에서 딥러닝을 사용하기 위해서입니다. MobileNet의 경량화 비결을 알기 위해선 Depthwise Separable Convolusion의 이해가 필요합니다.
Architecture
Depthwise Separable Convolution

Depthwise Separable Convolution은 위 그림과 같이 Depthwise Convolution과 Pointwise Convolution의 두 개의 별도 단계로 분리하여 계산 효율성을 크게 향상시키는 기법입니다.
Standard Convolution
$$ D_K \cdot D_K \cdot M \cdot M \cdot D_F \cdot D_F $$
\(D_K\) : 입력값 크기(W, H), \(M\) : 입력 채널 수, \(M\) : 출력 채널 수, \(D_F\) : 출력값 크기(W, H)
Depthwise Convolution
Depthwise Convolution의 경우 각 입력 채널에 대하여 3x3 Conv 하나의 필터가 연산을 수행하여 하나의 피쳐맵을 생성합니다. 입력 채널 수가 M개이면 M개의 피쳐맵을 생성합니다 (출력 채널 수 == 입력 채널 수). 각 채널마다 독립적으로 연산을 수행하여 Spatial Correlation을 계산하는 것입니다.
$$ D_K \cdot D_K \cdot M \cdot D_F \cdot D_F $$
\(D_K\) : 입력값 크기(W, H) , \(M\) : 입력 채널 수, \(D_F\) : 출력값 크기(W, H)
Pointwise Convolution
Potinwise Convolution은 Depthwise Convolution이 생성한 피쳐맵들을 1x1 Conv로 채널 수를 조정하는 작업을 말합니다.
1x1 Conv는 모든 채널에 대해 연산을 수행하므로, Cross Channel Correlation을 계산하게 되는 것입니다. 즉, 채널 간은 정보를 결합하고, 원하는 출력 채널 수로 조정할 수 있습니다.
$$ M \cdot N \cdot D_F \cdot D_F $$
\(M\) : 입력 채널 수, \(N\) : 출력 채널 수, \(D_F\) 출력값 크기(W, H)
연산량
$$ D_K \cdot D_K \cdot M \cdot D_F \cdot D_F + M \cdot N \cdot D_F \cdot D_F $$
Depthwise Separable Convolution의 연산량은 Depthwise Convolution의 연산량과 Poinwise Convolution 연산량의 합입니다.
이는 기존 Convolution 연산과 비교하였을 때 약 8~9배 적은 연산량을 가집니다.
Architecture

첫 번째 레이어는 Standard Conv를 사용하고 그 이후부터 Depthwise Conv와 Pointwise Conv를 번갈아가며 수행합니다.
feature map의 크기는 Stride를 2로 적용하여 크기를 절반으로 줄여주고 채널 수(필터 수)는 Ponitwise Conv를 수행할 때 지정합니다.
구현
import torch.nn as nn
class StandardConv(nn.Module):
def __init__(self, in_channels, out_channels, kernel_size, stride=1, padding=0):
super(StandardConv, self).__init__()
self.conv = nn.Conv2d(in_channels, out_channels, kernel_size, stride, padding)
def forward(self, x):
return self.conv(x)
standard_conv = StandardConv(in_channels=3, out_channels=64, kernel_size=3, padding=1)
class DepthwiseSeparableConv(nn.Module):
def __init__(self, in_channels, out_channels, kernel_size, stride=1, padding=0):
super(DepthwiseSeparableConv, self).__init__()
self.depthwise = nn.Conv2d(in_channels, in_channels, kernel_size, stride, padding, groups=in_channels)
self.pointwise = nn.Conv2d(in_channels, out_channels, 1)
def forward(self, x):
x = self.depthwise(x)
x = self.pointwise(x)
return x
depthwise_separable_conv = DepthwiseSeparableConv(in_channels=3, out_channels=64, kernel_size=3, padding=1)
Width Multiplier & Resolution Multiplier
Width Multiplier
기존의 MobileNet Architecture은 이미 작고 지연 시간이 짧지만 특정 상황에서는 더 작고 더 빠른 모델을 필요로 할 수도 있으니, Width Multiplier라고 불리는 파라미터 알파\(alpha\)를 도입합니다. 이 알파의 역할은 각 layer를 균일하게 더 얇게 만드는 것인데, input channel이 \(M\)이였다면 여기에 알파를 곱해 더 얇게 만들어줍니다.
$$ D_K \cdot D_K \cdot \alpha M \cdot D_F \cdot D_F + \alpha M \cdot \alpha N \cdot D_F \cdot D_F $$
보통 1, 0.75, 0.5, 0.25로 세팅하고 cost와 파라미터 수를 대략 알파의 거듭제곱만큼 감소시키는 효과를 가집니다.
Resolution Multiplier
Resolution Multiplier는 신경망의 계산 비용을 줄이기 위한 파라미터 \(\rho\) 입니다. \(\rho\)는 입력 이미지에 적용하여 해상도를 낮춥니다. 범위는 \(\rho \in (0,1]\)이고 네트워크 입력 해상도는 224, 192, 160, 128 입니다.
$$ D_K \cdot D_K \cdot \alpha M \cdot \rho D_F \cdot \rho D_F + \alpha M \cdot \alpha N \cdot \rho D_F \cdot \rho D_F $$
Experiments

FC를 사용한 모델과 Depthwise Separable을 사용한 MoblieNet의 결과입니다.
파라미터는 많이 감소하였으나, 정확도 부분은 약 1%만 감소했음을 확인할 수 있습니다.

당시 사용되던 모델들과의 비교입니다. MobileNet이 VGG만큼 정확하지만 파라미터 값도 상당히 적음을 확인할 수 있습니다.
마무리
MobileNet은 정확도를 조금 내주고 더 효율적인 모델로 설계했습니다. 또한 하이퍼파라미터를 통해 다양한 환경과 요구사항에 맞춰 유연하게 조정할 수 있다는 장점을 가지고 있습니다. 고려해야할 점으로 해상도를 낮게 설정할 경우 작은 객체나 세밀한 특징을 검출하기 어려워 질 수 있겠다는 생각을 했습니다.
참고
[1] https://arxiv.org/pdf/1704.04861v1
[2] https://dacon.io/forum/406019
[3] https://velog.io/@twinjuy/MobileNet-%EB%85%BC%EB%AC%B8%EB%A6%AC%EB%B7%B0
'Paper Review' 카테고리의 다른 글
| [EfficientNet] Rethinking Model Scaling for Convolutional Neural Networks (0) | 2024.07.11 |
|---|---|
| [SENet] Squeeze and Excitation Networks (0) | 2024.07.10 |
| [GAN] Generative Adversarial Nets (0) | 2024.01.30 |
| [SegNet] A Deep ConvolutionalEncoder-Decoder Architecture for ImageSegmentation (0) | 2023.06.08 |
| [DeConvNet] Learning Deconvolution Network for Semantic Segmentation (0) | 2023.06.08 |
