SENet
기존의 네트워크들은 깊이(Depth)를 늘리거나 층(Layer)의 관계를 수정하여 성능을 끌어올리는 방법을 생각했습니다.
SENet은 채널 간의 상호작용(Channel Relationship)에 초점을 맞추어 성능을 끌어올린 모델입니다. 즉, 채널 간의 특징을 파악하고 채널 사이의 상호 종속 특징들을 명시적으로 모델링하면서 그에 맞게 재조정하는 과정을 거칩니다.
이를 위해 새로운 형태의 Architecture Unit인 SE Block을 이 논문에서 소개합니다.
SE Block
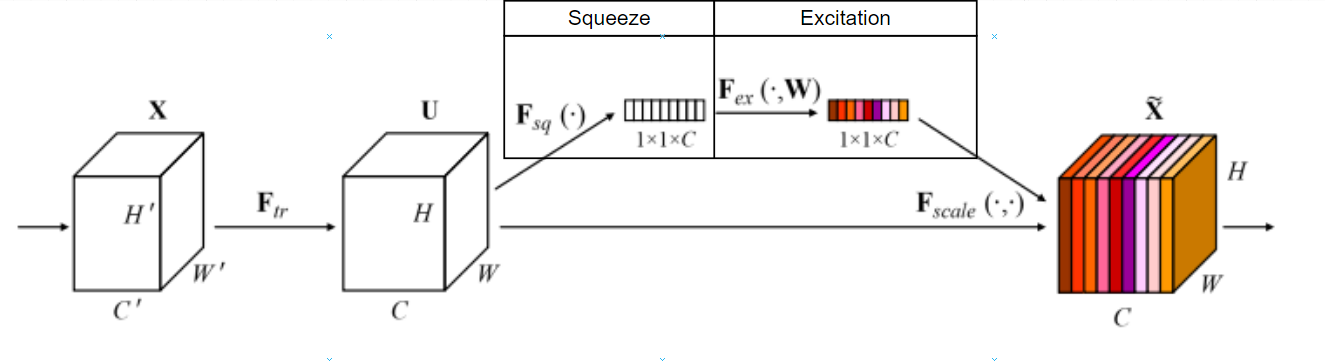
SE Block은 Squeeze와 Excitation으로 크게 2단계를 거쳐 채널 간의 상호작용을 고려하게 됩니다.
Squeeze는 "짜내다"라는 뜻으로 많은 양의 정보를 압축하는 의미가 있으며, 논문에서는 Global Information Embedding 이라는 이름을 설명합니다.
Excitation는 논문에서 적절하게 recalibration(재조정) 하는 것이다 라고 설명합니다.
Squeeze: Global Information Embedding
Squeeze 작업은 각 채널의 특징들을 연산을 통해 하나의 값으로 압축하는 것입니다.
논문에서는 그림과 같이 Feature Map \(U\)를 입력으로 받아 (H, W, C)의 크기를 Global Average Pooling 연산을 통해 (1, 1, C)로 압축합니다.
Global Average Pooling은 Feature Map의 한 채널에 해당하는 픽셀의 값을 모두 더한 후, H x W로 나누어 압축합니다.
Feature Map을 C개의 채널을 가지고 있기 때문에, 모두 연결하면 \(z\) (1, 1, C)가 됩니다.
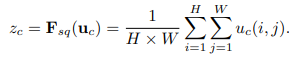
이 기능은 채널별 정보에서 위치 정보는 버리고 물체 정보만 남기는 역할이라고도 생각할 수 있습니다.
Excitation: Adaptive Recalibration
Excitation 작업은 채널별 압축한 정보들을 사용하여 채널별 중요도를 계산합니다.
SENet에서는 이를 Fully Connected 1 \(\rightarrow\) ReLU \(\rightarrow\) Fully Connected 2 \(\rightarrow\) Sigmoid 순서로 구성했습니다.
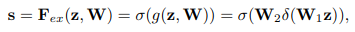
\(W\) : FC 연산의 가중치, \(\delta\) : ReLU, \(\sigma\) : Sigmoid
1. FC1에서 (1, 1, C)를 입력으로 받아 C개의 채널을 C / r 개의 채널로 축소합니다. (*r 은 하이퍼파라미터)
2. C / r 개로 축소된 벡터를 ReLU(비선형성 추가)를 거쳐 FC2로 전달합니다.
3. FC2는 다시 채널을 C개로 되돌립니다.
4. Attention Score(중요도)를 표현하기 위해 Sigmoid를 거쳐 [0~1) 범위의 값을 지니도록 합니다.
Scale
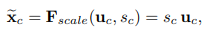
Squeeze와 Excitation를 거쳐 나온 가중치 \(S\)들을 \(U\)와 곱하여 \(U\)를 재조정합니다.
즉, 각 채널 간의 특징을 토대로 채널 간의 가중치를 구해 이에 따라 채널 값의 중요도를 재구성합니다.
SE-Inception & SE-ResNet
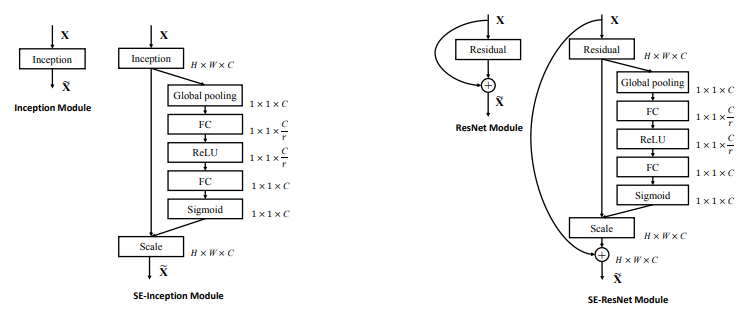
SE Block은 각각의 Conv 연산의 전처리 \(F_{tr} : X^{H' \cdot W' \cdot C'} \rightarrow U^{H \cdot W \cdot C}\) 이후 삽입되어 기존의 네트워크와도 자연스럽게 연결할 수 있습니다.
논문의 저자는 Inception의 여러 사이즈의 Conv Layer를 거친 후 다양한 정보가 담긴 특징 맵들의 정보들은 SE Block과의 시너지가 클 것이라 생각 했는데 결과는 ResNet과의 결합이 더 좋았다고 합니다.
Experiments
Image Classification 실험의 결과입니다.
1. ImageNet
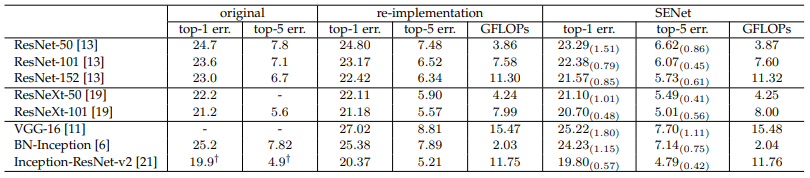
2. CIFAR10

3. CIFAR100

3개의 데이터셋에서 SE 모듈을 추가했을 때 성능이 향상되는 것을 확인할 수 있습니다.
Hyperparameter
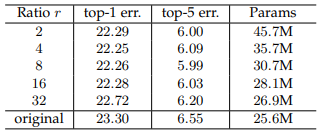
Reduction Ratio \(r\)
\(r\) 값의 조정으로 인해 SE Block의 성능과 복잡도가 다양해집니다.
Squeeze Operator
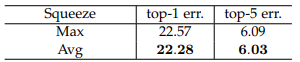
본 논문에서는 Global Average Pooling(GAP) 연산을 주로 사용했는데, Global Max Pooling(GMP) 연산의 결과를 보여줍니다.
Excitation Operator
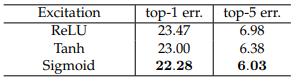
비선형 함수를 선택하는 것에 대해서 실험한 결과를 보여줍니다.
Different Stages
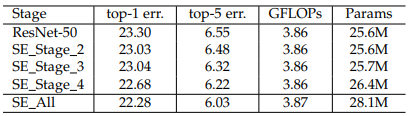
ResNet50에서 SE Block들을 각각 다른 Stage에서 합치는 것이 어떤 영향을 끼치는지 실험한 결과를 보여줍니다.
Role of Squeeze
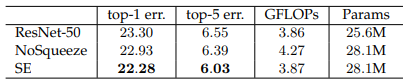
저자들이 Squeeze의 실효성을 확인하고 싶어서 Squeeze의 기능을 없애서 Excitation만으로 구성하되, 공평한 실험을 위해 연산 파라미터 개수를 맞췄습니다. (GAP 연산은 제거하고, FC 연산을 1x1 Conv로 대체)
위 결과를 통해 Squeeze 기능은 효과가 있다고 말할 수 있습니다.
Role of Excitation
똑같이 저자들은 Excitation의 실효성을 확인하고자 합니다.
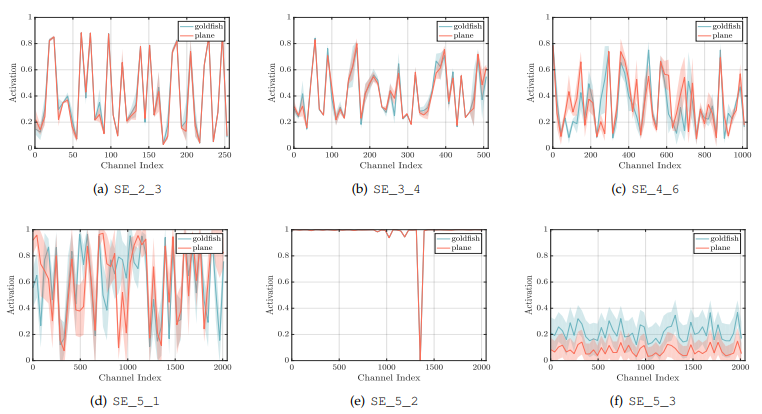
위 그림은 ImageNet의 glodfish, plane 클래스에 대해 50개의 샘플의 Activation 평균값을 나타낸 그래프입니다.
초기 Layer에서는 클래스와 무관하게 분포가 비슷합니다. 이는 초기 단계에서 Feature Channel이 다른 클래스에서도 서로 공유가 된다는 것입니다.
Layer가 깊어질 수록 점점 class에 따라 값들이 구체화 되어 갑니다.
마지막 Layer (f) plot은 class마다 분포가 다르지만, 패턴이 유사한 것을 볼 수 있습니다.
이 결과는 후반 레이어 e, f는 SE Block의 효과가 매우 미미하고 Computational Cost만 올리기 때문에 제거하는 것이 좋을 것 같다고 합니다.
구현
import torch
import torch.nn as nn
class SEBlock(nn.Module):
def __init__(self, channel, reduction=16):
super(SEBlock, self).__init__()
self.avg_pool = nn.AdaptiveAvgPool2d(1)
self.fc = nn.Sequential(
nn.Linear(channel, channel // reduction, bias=False),
nn.ReLU(inplace=True),
nn.Linear(channel // reduction, channel, bias=False),
nn.Sigmoid()
)
def forward(self, x):
b, c, _, _ = x.size()
y = self.avg_pool(x).view(b, c)
y = self.fc(y).view(b, c, 1, 1)
return x * y.expand_as(x)
참고
[1] https://arxiv.org/pdf/1709.01507
[2] https://deep-learning-study.tistory.com/539
[3] https://inhovation97.tistory.com/48
[4] https://ffighting.net/deep-learning-paper-review/vision-model/senet/
[5] https://velog.io/@pre_f_86/SENet-%EB%85%BC%EB%AC%B8-%EB%A6%AC%EB%B7%B0
'Paper Review' 카테고리의 다른 글
SENet
기존의 네트워크들은 깊이(Depth)를 늘리거나 층(Layer)의 관계를 수정하여 성능을 끌어올리는 방법을 생각했습니다.
SENet은 채널 간의 상호작용(Channel Relationship)에 초점을 맞추어 성능을 끌어올린 모델입니다. 즉, 채널 간의 특징을 파악하고 채널 사이의 상호 종속 특징들을 명시적으로 모델링하면서 그에 맞게 재조정하는 과정을 거칩니다.
이를 위해 새로운 형태의 Architecture Unit인 SE Block을 이 논문에서 소개합니다.
SE Block

SE Block은 Squeeze와 Excitation으로 크게 2단계를 거쳐 채널 간의 상호작용을 고려하게 됩니다.
Squeeze는 "짜내다"라는 뜻으로 많은 양의 정보를 압축하는 의미가 있으며, 논문에서는 Global Information Embedding 이라는 이름을 설명합니다.
Excitation는 논문에서 적절하게 recalibration(재조정) 하는 것이다 라고 설명합니다.
Squeeze: Global Information Embedding
Squeeze 작업은 각 채널의 특징들을 연산을 통해 하나의 값으로 압축하는 것입니다.
논문에서는 그림과 같이 Feature Map \(U\)를 입력으로 받아 (H, W, C)의 크기를 Global Average Pooling 연산을 통해 (1, 1, C)로 압축합니다.
Global Average Pooling은 Feature Map의 한 채널에 해당하는 픽셀의 값을 모두 더한 후, H x W로 나누어 압축합니다.
Feature Map을 C개의 채널을 가지고 있기 때문에, 모두 연결하면 \(z\) (1, 1, C)가 됩니다.
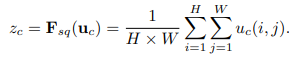
이 기능은 채널별 정보에서 위치 정보는 버리고 물체 정보만 남기는 역할이라고도 생각할 수 있습니다.
Excitation: Adaptive Recalibration
Excitation 작업은 채널별 압축한 정보들을 사용하여 채널별 중요도를 계산합니다.
SENet에서는 이를 Fully Connected 1 \(\rightarrow\) ReLU \(\rightarrow\) Fully Connected 2 \(\rightarrow\) Sigmoid 순서로 구성했습니다.
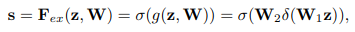
\(W\) : FC 연산의 가중치, \(\delta\) : ReLU, \(\sigma\) : Sigmoid
1. FC1에서 (1, 1, C)를 입력으로 받아 C개의 채널을 C / r 개의 채널로 축소합니다. (*r 은 하이퍼파라미터)
2. C / r 개로 축소된 벡터를 ReLU(비선형성 추가)를 거쳐 FC2로 전달합니다.
3. FC2는 다시 채널을 C개로 되돌립니다.
4. Attention Score(중요도)를 표현하기 위해 Sigmoid를 거쳐 [0~1) 범위의 값을 지니도록 합니다.
Scale
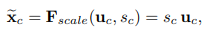
Squeeze와 Excitation를 거쳐 나온 가중치 \(S\)들을 \(U\)와 곱하여 \(U\)를 재조정합니다.
즉, 각 채널 간의 특징을 토대로 채널 간의 가중치를 구해 이에 따라 채널 값의 중요도를 재구성합니다.
SE-Inception & SE-ResNet

SE Block은 각각의 Conv 연산의 전처리 \(F_{tr} : X^{H' \cdot W' \cdot C'} \rightarrow U^{H \cdot W \cdot C}\) 이후 삽입되어 기존의 네트워크와도 자연스럽게 연결할 수 있습니다.
논문의 저자는 Inception의 여러 사이즈의 Conv Layer를 거친 후 다양한 정보가 담긴 특징 맵들의 정보들은 SE Block과의 시너지가 클 것이라 생각 했는데 결과는 ResNet과의 결합이 더 좋았다고 합니다.
Experiments
Image Classification 실험의 결과입니다.
1. ImageNet

2. CIFAR10

3. CIFAR100

3개의 데이터셋에서 SE 모듈을 추가했을 때 성능이 향상되는 것을 확인할 수 있습니다.
Hyperparameter
Reduction Ratio \(r\)
\(r\) 값의 조정으로 인해 SE Block의 성능과 복잡도가 다양해집니다.

Squeeze Operator

본 논문에서는 Global Average Pooling(GAP) 연산을 주로 사용했는데, Global Max Pooling(GMP) 연산의 결과를 보여줍니다.
Excitation Operator

비선형 함수를 선택하는 것에 대해서 실험한 결과를 보여줍니다.
Different Stages

ResNet50에서 SE Block들을 각각 다른 Stage에서 합치는 것이 어떤 영향을 끼치는지 실험한 결과를 보여줍니다.
Role of Squeeze

저자들이 Squeeze의 실효성을 확인하고 싶어서 Squeeze의 기능을 없애서 Excitation만으로 구성하되, 공평한 실험을 위해 연산 파라미터 개수를 맞췄습니다. (GAP 연산은 제거하고, FC 연산을 1x1 Conv로 대체)
위 결과를 통해 Squeeze 기능은 효과가 있다고 말할 수 있습니다.
Role of Excitation
똑같이 저자들은 Excitation의 실효성을 확인하고자 합니다.

위 그림은 ImageNet의 glodfish, plane 클래스에 대해 50개의 샘플의 Activation 평균값을 나타낸 그래프입니다.
초기 Layer에서는 클래스와 무관하게 분포가 비슷합니다. 이는 초기 단계에서 Feature Channel이 다른 클래스에서도 서로 공유가 된다는 것입니다.
Layer가 깊어질 수록 점점 class에 따라 값들이 구체화 되어 갑니다.
마지막 Layer (f) plot은 class마다 분포가 다르지만, 패턴이 유사한 것을 볼 수 있습니다.
이 결과는 후반 레이어 e, f는 SE Block의 효과가 매우 미미하고 Computational Cost만 올리기 때문에 제거하는 것이 좋을 것 같다고 합니다.
구현
import torch
import torch.nn as nn
class SEBlock(nn.Module):
def __init__(self, channel, reduction=16):
super(SEBlock, self).__init__()
self.avg_pool = nn.AdaptiveAvgPool2d(1)
self.fc = nn.Sequential(
nn.Linear(channel, channel // reduction, bias=False),
nn.ReLU(inplace=True),
nn.Linear(channel // reduction, channel, bias=False),
nn.Sigmoid()
)
def forward(self, x):
b, c, _, _ = x.size()
y = self.avg_pool(x).view(b, c)
y = self.fc(y).view(b, c, 1, 1)
return x * y.expand_as(x)
참고
[1] https://arxiv.org/pdf/1709.01507
[2] https://deep-learning-study.tistory.com/539
[3] https://inhovation97.tistory.com/48
[4] https://ffighting.net/deep-learning-paper-review/vision-model/senet/
[5] https://velog.io/@pre_f_86/SENet-%EB%85%BC%EB%AC%B8-%EB%A6%AC%EB%B7%B0
