DETR
ViT는 Transformer 구조를 활용하여, Classification을 수행하였습니다. 그럼, Object Detection은 어떻게 할까요 ?
바로 DETR (End-to-End Object Detection with Transformers) 논문을 통해 해결 방법을 확인할 수 있습니다.
DETR은 end-to-end로 object detection을 수행하면서 높은 성능을 보입니다.
Abstract
- Object Detection을 direct set prediction problem(직접적인 집합 예측 문제)로 보는 방법을 제시
- NMS와 같이 후처리, anchor generation 같이 사전 정의해야하는 pipeline을 제거
- Bi-partite Matching(이분매칭)과 Transformer Encoder-Decoder 구조로 구성
- 학습된 객체 Query 집합을 사용하여 객체간 관계와 전체 이미지 맥락을 추론하여 병렬적으로 추론
- 구조적으로 간단하고, 별도의 라이브러리를 사용하지 않음
- Faster R-CNN과 비슷한 정확도와 처리 시간
- Object Detection 외에 Segmentation으로 쉽게 확장 가능
Preliminaries
들어가기에 앞서 본 논문을 제대로 이해하기 위한 사전지식을 간단하게 살펴봅니다.
(Direct Set Prediction Problem, Hungarian Algorithm, Bounding Box Loss)
Direct Set Prediction Problem
본 논문에서는 Object Detection을 bounding box와 category label이라는 set \(G = {(B_0, C_0), (B_1, C_1), \cdots, (B_n, C_n)}\)을 예측하는 task로 정의합니다.
기존의 Object Detection 방법은 다수의 proposal, anchor box, window center 등을 기반으로 set을 찾는 '간접적인 방법'에 기반을 두어 동작합니다. 반면, 이 논문에서는 복잡한 pipeline을 간소화하여 set을 예측하는 '직접적인 방법'을 제안합니다.


기존의 Object Detection 방법은 pre-defined(사전정의된) anchor를 사용합니다. 이는 이미지 내 고정된 지점(grid cell)마다 다양한 scale, aspect ratio를 가진 anchor를 생성합니다. 그리고 이 anchor를 기반으로 예측한 bounding box와 ground truth를 비교하여, IoU 값이 threshold 이상일 경우 긍정, 이하일 경우 부정 sample로 간주하여 bounding box regression을 수행합니다. 이처럼 threshold를 기준으로 독립적으로 prediction을 수행하기 때문에 하나의 ground truth에 다수의 bounding box가 매칭됩니다.
이렇게 다수의 anchor를 생성함으로써, 다양한 크기와 형태의 객체를 효과적으로 검출하는 것이 가능합니다. 하지만, 이러한 특징은 near-duplicate한 예측, redundant한 예측을 제거하기 위해 NMS(Non-Maximum Suppression)과 같은 post-processing(후처리) 과정이 반드시 필요합니다.
DETR에서는 이러한 사전정의, 후처리 과정을 제거하고, Transformer로 End-to-End로 학습이 가능한 방법을 Hungarian Algorithm을 사용하여 해결합니다.
Hungarian Algorithm
Hungarian Algorithm은 두 집합 사이의 일대일 대응 시 가장 비용이 적게 드는 bi-partite matching(이분 매칭)을 찾는 알고리즘입니다. 조금 더 자세히 들어가면, Hungarian Algorithm은 어떠한 집합 \(I\)와 matching 대상인 집합 \(J\)가 있으며, \(i \in J\)를 \(j \in J\)에 matching 하는데 드는 비용을 \(c(i,j)\)라고 할 때, \(\sigma : I \rightarrow J\)로의 일대일 대응 중에서 가장 적은 cost가 드는 matching에 대한 permutation \(\sigma\)를 찾는 것입니다. 여기서 \(\sigma\)는 matching시 최적의 순서에 대한 index를 의미합니다.
DETR에서는 predicted bounding box를 ground truth에 1:1로 matching 시키기 위해 Hungarian Algorithm을 사용합니다. 다음 예시는 이미지 내 두 객체가 있을 때, predicted bounding box에서 ground truth를 matching하는 문제입니다.
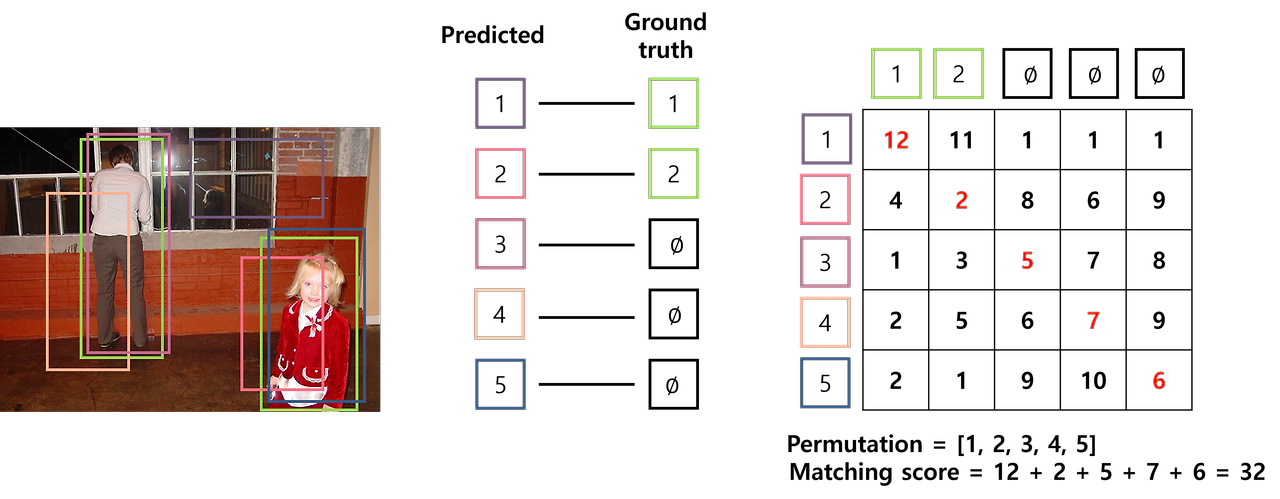
cost에 대한 행렬을 취와 같이 표현할 수 있습니다. 행렬의 행은 predicted bounding box를, 열은 ground truth를 의미하며, 행렬의 각 요소는 predicted bounding box가 ground truth로 matching 되었을 때의 cost를 의미합니다. 지금처럼 permutation (\(\sigma\))이 [1,2,3,4,5]인 경우, cost가 32인 것을 확인할 수 있습니다.
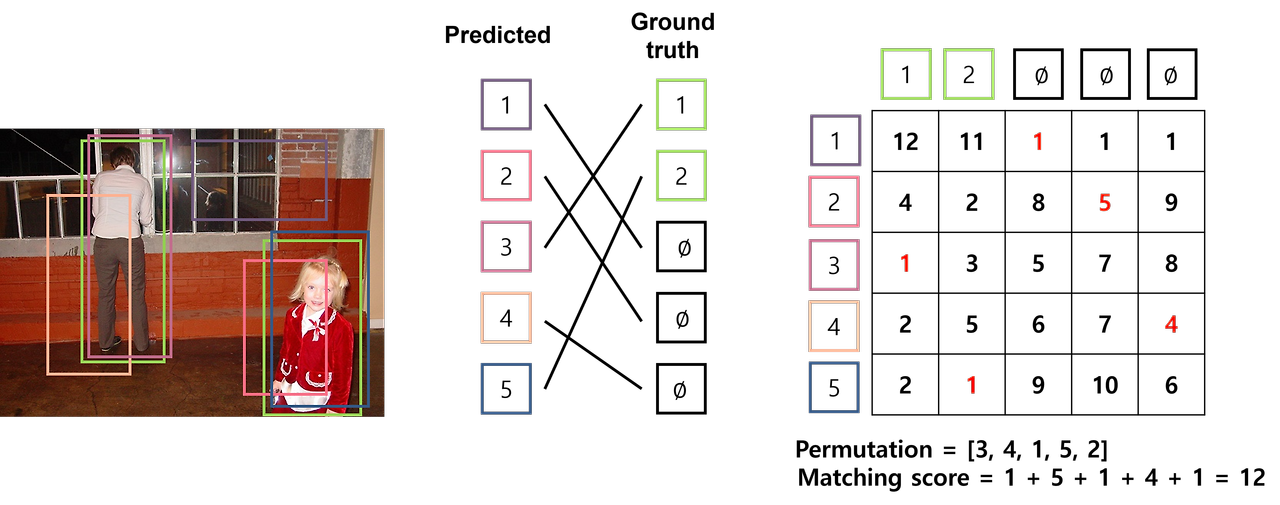
반면, Hungarian Algorithm을 통해 permutation을 [3,4,1,5,2]로 설정할 경우, cost가 12로 상대적으로 매우 낮은 값을 얻을 수 있습니다. 즉, Hungarian Algorithm은 cost에 대한 행렬을 입력받아, matching cost가 최소인 permutation (\(\sigma\))을 출력합니다. Hungarian Algorithm의 동작은 Gazelle and Computer Science님의 블로그에서 자세히 확인할 수 있습니다.
Bounding Box Loss
Hungarian Algorithm 연산과 loss 계산 시 사용되는 bounding box loss에 대해 살펴보겠습니다. 기존의 방법은 anchor를 기반으로 예측을 수행하기 때문에 predicted bounding box가 ground truth와의 범위가 크게 벗어나지 않습니다. 반면, DETR은 사전에 직접 정의한 값 없이 bounding box를 예측하기 때문에 예측하는 값의 범주가 상대적으로 큽니다. 따라서 절대적인 거리를 측정하는 L1 Loss를 사용할 경우, 상대적인 오차는 비슷하지만, 크기가 큰 box와 작은 box는 서로 다른 범위의 loss를 가지게 될 것입니다. 이러한 문제를 해결하기 위해 본 논문에선s L1 Loss와 Generalized IoU(GIoU) Loss를 함께 사용합니다.
$$ IoU = \frac{| b_{\sigma (i)} \cap \hat{b_i} |}{| b_{\sigma (i)} \cup \hat{b_i} |} $$
$$ GIoU = IoU - \frac{| B(b_{\sigma (i)}, \hat{b_i}) \backslash b_{\sigma (i)} \cup \hat{b_i} |}{| B(b_{\sigma (i)}, \hat{b_i}) |} $$
$$ \mathcal{L}_{iou} (b_{\sigma (i)}, \hat{b_i}) = 1 - GIoU $$
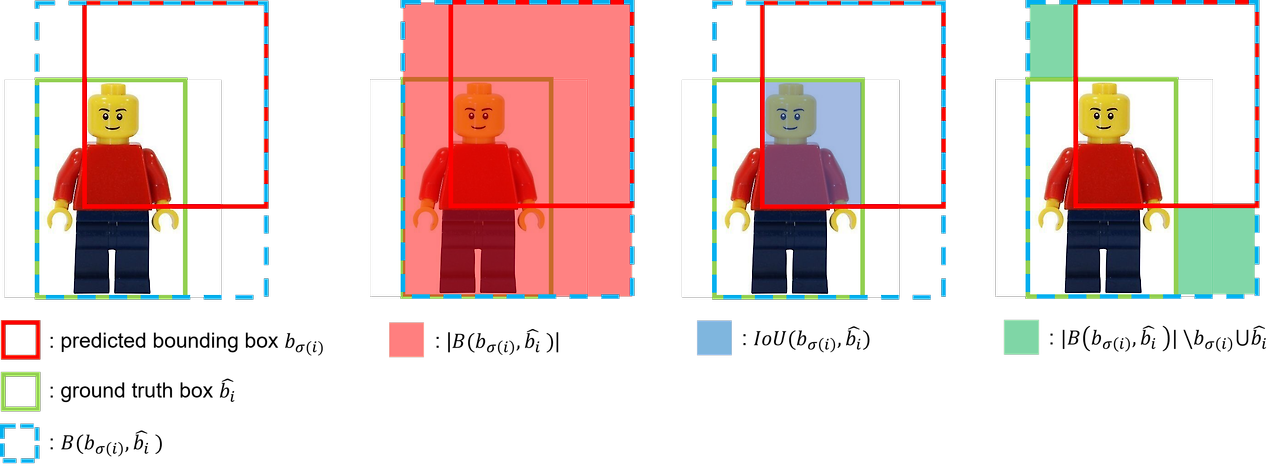
Generalized IoU(GIoU) loss는 두 box 사이의 IoU값을 활용한 loss로 scale-invariant하다는 특징이 있습니다. 즉, 절대적인 크기에 상관없이 측정이 가능하다는 것 입니다. GIoU를 구하기 위해선 predicted bounding box, \(b_{\sigma (i)}\)와 ground truth box, \(\hat{b_i}\)를 둘러싸는 가장 작은 box, \(B(b_{\sigma (i)}, \hat{b_i})\)를 구합니다. 이 때 predicted bounding box와 ground truth box가 많이 겹칠수록 \(B\)가 작아지며, 두 box가 멀어질수록 \(B\)가 커집니다. \(IoU( b_{\sigma (i)}, \hat{b_i} )\)는 두 box 사이의 IoU를 의미하며, \( \frac{| B(b_{\sigma (i)}, \hat{b_i}) \backslash b_{\sigma (i)} \cup \hat{b_i} |}{| B(b_{\sigma (i)}, \hat{b_i}) |} \)는 \(B\)에서 predicted bounding box와 ground truth box를 합한 영역을 뺀 영역에 해당합니다. 이 때 \(GIoU\)는 -1 ~ 1 사이의 값을 가지며, \(GIoU\)를 loss로 사용할 때 \(1 - GIoU\)로 사용하여 0 ~ 2 사이의 값을 가지게 됩니다.
$$ \mathcal{L}_{box} ( b_{\sigma (i)}, \hat{b_i} ) = \lambda_{iou} \mathcal{L}_{iou} ( b_{\sigma (i)}, \hat{b_i} ) + \lambda_{L1} || b_{\sigma (i)} - \hat{b_i} ||_1 $$
위 수식은 L1 Loss와 GIoU Loss를 사용한 전체 Bounding Box Loss입니다. 이 수식에서 \(\lambda_{iou}\)와 \(\lambda_{L1}\)은 두 term 사이를 조정하는 scalar hyperparameter입니다.
The DETR model
본 논문에서는 object detection 시 direct set prediction을 위해 두 가지 요소가 필수적이라고 합니다.
[1] predicted bounding box와 ground truth box 사이의 unique matching을 가능하도록 하는 set prediction loss
[2] 한 번의 forward pass로 object 집합들을 예측하고, 관계를 예측하는 구조
Object detection set prediction loss

조건 [1]을 충족하기 위해 loss를 계산하는 과정은 두 단계로 구분됩니다.
1) predicted bounding box와 ground truth box 사이의 unique한 matching을 수행
2) matching된 결과를 기반으로 hungarian loss를 연산
기존의 연구는 수 천개의 anchor를 생성하여, 객체를 예측하기 위한 proposals로 사용하는데, 이는 객체가 얼마나 있을지 알 수 없기 때문입니다. 본 논문에서 제안한 DETR은 고정된 크기의 \(N\)개의 prediction을 수행함으로써, 수많은 anchor를 생성하는 과정을 우회합니다. \(N\)은 일반적으로 이미지 내 존재하는 객체의 수보다 훨씬 큰 수로 지정합니다. 이를 통해 적은 수의 prediction을 수행하여 기존의 연구 방법보다 unique matching을 쉽게 수행할 수 있습니다.
\(y\)는 객체에 대한 ground truth set이며 \(\hat{y}\)는 \(N\)개의 prediction입니다. 이 때 \(y\)의 크기 역시 \(N\)개이며, 객체의 수를 제외한 나머지는 \(\varnothing\)(no object)로 간주합니다. 즉 \(N\)이 100이고, 이미지 내 객체의 수가 3개이면 \(y\)에서 97개는 \(\varnothing\)으로 pad 됩니다. 이 때 두개의 set에 대하여 bi-partite matching을 수행하기 위해 아래의 cost를 최소화할 수 있는 \(N\)개의 permutation \(\sigma\)을 탐색합니다.
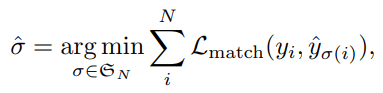
이 때 \(\mathcal{L}_{match} (y_i, \hat{y_{\sigma (i)}}\)는 ground truth \(y_i\)와 index \(\sigma (i)\)에 대한 prediction 사이의 pair-wise mathcing cost 입니다. 이러한 matching cost는 class prediction과 predicted bounding box와 ground truth box 사이의 similarity(유사도)를 모두 고려합니다. ground truth의 \(i\)번째 요소인 \(y_i = (c_i, b_i)\)에서 \(c_i\)는 target class label을 의미하며, \(b_i \in [0,1]^4\)는 ground truth box의 좌표와 이미지 크기에 상대적인 width, height를 의미합니다. index가 \(\sigma(i)\)인 prediction 결과에 대해 class probability를 \(\hat{p_{\sigma (i)} (c_i)}\)로, predicted box를 \(\hat{b_{\sigma (i)}}\)로 정의합니다. 이 때 matching cost를 다음과 같은 수식으로 표현할 수 있습니다.
$$ \mathcal{L}_{match} ( y_i, \hat{y}_{\sigma (i)} ) = -1_{c_i \neq \emptyset} \hat{p}_{\sigma (i)} (c_i) + 1_{ c_i \neq \emptyset } \mathcal{L}_{box} (b_i, \hat{b}_{\sigma (i)}) $$
이 때 \(\mathcal{L}_{box}\)는 사전지식에서 언급한 bounding box loss 입니다.
$$ \mathcal{L}_{box} ( b_i, \hat{b}_{\sigma (i)} ) = \lambda_{iou} \mathcal{L}_{iou} ( b_i, \hat{b}_{\sigma (i)} ) + \lambda_{L1} || b_i - \hat{b}_{\sigma (i)} ||_1 $$
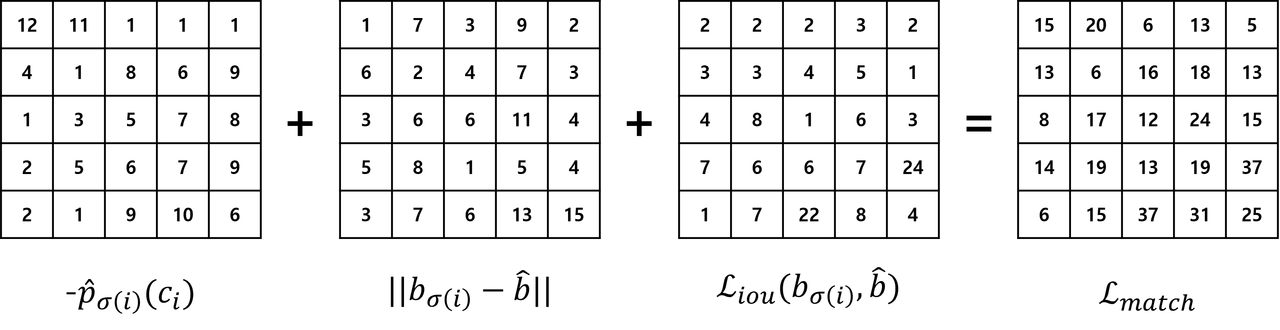
predicted bounding box와 ground truth box에 대한 matching cost 행렬은 위와 같이 표현할 수 있습니다. 이러한 최적의 할당은 Hungarian Algorithm에 의해 효율적으로 연산됩니다. 이와 같은 matching 과정은 기존의 heuristic한 방법과 비슷한 역할을 수행합니다.
앞선 과정을 통해 matching된 pair를 기반으로 loss funcing인 Hungarian Loss를 계산합니다. 이 때 Loss는 class loss와 box loss로 구성됩니다. class loss는 prediction에 대한 negative log-likelihood를 구합니다. box loss는 사전지식에서 언급한 L1 loss와 generalized IoU loss를 결합하여 사용합니다.
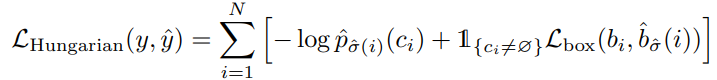
\(\hat{\sigma}(i)\)는 이전 단계에서 구한 optimal assignment입니다. 실제 학습 시에는 예측하는 객체가 없는 경우인 \(c_i = \varnothing\)에 대하여 log-probability를 1/10로 down-weight 합니다. 이는 실제로 객체를 예측하지 않는 negative sample 수가 매우 많아 class imblance를 위해 해당 sample에 대한 영향을 감소시키기 위함입니다.
Architecture
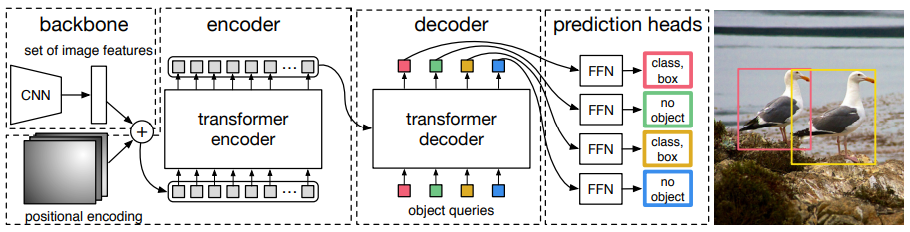
DETR는 CNN Backbone, Transformer Encoder-Decoder, FFN(Feed Foward Network) 3가지로 구성되어 있습니다.
Backbone
입력 이미지 \( x_{ img } \in \mathbb{R}^{ 3 \times H_0 \times W_0 } \)를 CNN backbone에 입력하여 feature map \(f \in \mathbb{R}^{ C \times H \times W \)를 추출합니다. 이 때 \(C = 2048\) 이며, \(H, W = \frac{H_0}{32}, \frac{W_0}{32}\) 를 사용합니다.
Transformer Encoder
이후 계산량을 줄이기 위해 1x1 Conv를 통해 feature map \(f\)의 채널 차원을 \(C\)에서 더 작은 차원 \(d\)로 줄여 새로운 feature map \(z_0 \in \mathbb{R}^{d \times H \times W} \)를 생성합니다. 그리고, Encoder는 시퀀스를 입력으로 받기 때문에, \(z_0\)의 공간 차원(spatial dimension)을 1차원으로 축소(collapse = flatten)하여 크기를 \(d \times H \cdot W\)으로 변경합니다. 각각의 Encoder Layer는 multi-head self-attention module과 feed forward network(FFN)으로 구성되어 있습니다. Transformer 구조는 입력 embedding의 순서와 상관없이 같은 출력값을 생성하는 permutation-invariant 속성이 있기 때문에 encoder layer 입력 전에 입력 embedding에 positional encoding을 더해줍니다.
Transformer Decoder
Transformer Decoder는 masking을 통해 다음 token을 예측하는 autoregressive 방법을 사용하는 반면, DETR의 decoder는 \(N\)개의 object에 대한 정보를 한번에 출력합니다. decoder 역시 permutation-invariant하기 때문에 \(N\)개의 다른 결과를 얻기 위해 입력으로 받는 embedding으로 object queries라고 불리는 learnt positional encoding을 사용합니다.
하나의 object query는 object query feature과 object query positional embedding으로 구성되어 있습니다. object query feature는 decoder에 initial input으로 사용되어, decoder layer를 거치면서 학습됩니다. object query embedding은 decoder layer에서 attention 연산 시 모든 query feature에 더해집니다.
query feature는 학습 시작 시 0으로 초기화(zero-initialized)되며, query positional embedding은 학습 가능(learnable)합니다. 이러한 object query는 길이가 \(N\)으로, decoder에 의해 output embedding으로 변환되며 이후 FFN을 통해 각각 독립적으로 box coordinate와 class label로 decode 됩니다. 이는 object query는 하나의 객체를 예측하는 region proposal에 대응된다고 볼 수 있습니다. 즉, object qeuries는 \(N\)개의 객체를 예측하기 위한 일종의 prior knowledge로도 볼 수 있습니다.
Encoder와 유사하게 object qeury를 각 attention layer의 입력에 더해줍니다. 이 때 embedding은 self-attention과 encoder-decoder attention을 통해 이미지 내 전체 문맥(context)에 대한 정보를 사용합니다. 이를 통해 객체 사이의 pair-wise relation을 포착하여 객체간의 전역적(global)인 정보를 모델링하는 것이 가능해집니다.
Prediction Feed-Forward Networks (FFNs)
Decoder에서 출력한 output embedding을 3개의 linear layer와 ReLU activation function으로 구성된 FFN에 입력하여 최종 예측을 수행합니다. FFN은 이미지에 대한 class label과 bounding box의 좌표(normalized coordinate, width, height)를 softmax를 통해 예측합니다. 이 때 예측하는 class label 중 \(\varnothing\)은 객체가 포착되지 않은 경우로, 'background' class를 의미합니다.
Auxiliary Decoding Losses
학습 시, 각 decoder layer마다 FFN을 추가하여 auxiliary loss를 구합니다. 이러한 보조적인 loss를 사용할 경우 모델이 각 class별로 올바른 수의 객체를 예측하도록 학습시키는데 도움을 준다고 합니다. 이렇게 추가한 FFN은 서로 파라미터를 공유하며, FFN 입력 전에 사용하는 layer normalized layer에도 공유합니다.
Experiments
Comparison with Faster R-CNN
COCO dataset에 대한 실험 결과, DETR은 같은 수의 파라미터로 Faster R-CNN과 비슷한 수준의 성능을 보였습니다.
Ablations

Number of encoder layers
Encoder 수로 ablation study를 진행한 결과 encoder를 전혀 사용하지 않으면 성능이 3.9% 감소했습니다. 논문 저자들은 Encoder가 global scene reasoning을 통해 객체를 분리하는 작업을 수행하기 때문이라고 가정합니다. Encoder Layer의 activation map을 시각화한 그림을 통해 알 수 있습니다.
Number of decoder layers
Decoder를 추가할수록 성능이 향상되었습니다. 하나의 Decoder만을 사용한 경우 output에 대한 cross-correlation을 연산하지 못하기 때문에 duplicate prediction이 발생하였습니다. decoder의 attention map을 시각화한 결과, 다음 그림과 같이 다소 local하게 객체를 잘 포착하고 있습니다. 저자들은 encoder가 global attention을 통해 객체를 배경으로부터 분리했기 때문에 Decoder는 객체의 경계 부분만 포착하면 될 것이라고 가정합니다.

Importance of FFN
Transformer에서 FFN을 제거하고 attention layer만 사용한 경우, AP 값이 2.3% 감소했습니다.
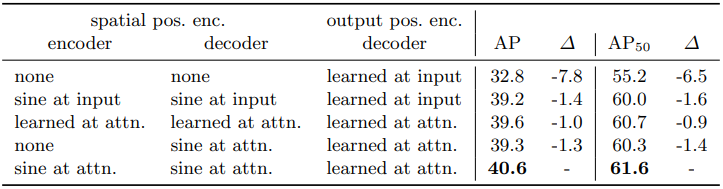
Importance of positional encoding
spatial positional encoding을 사용하지 않고 decoder에 object queires만 사용한 결과 베이스라인에 비해 AP 값이 7.8% 감소했습니다. 또한 decoder에 단 한 번 object query를 입력한 결과 모든 layer마다 object query를 더해주었을 때에 비해 AP 값이 1.4% 감소했습니다.
Loss ablations
L1 loss와 GIoU loss 에 대한 ablation 실험을 수행한 결과, GIoU loss만 사용한 경우 성능이 0.8% 정도만 감소했으나, L1 loss만 사용한 경우 성능이 5% 가까이 감소했습니다. 이를 통해 GIoU loss가 사실상 bounding box loss에 대한 기여도가 매우 높음을 알 수 있습니다.
Conclusion
Transformer를 Object Detection에 처음 적용한 논문으로, 많은 후속 논문이 나왔습니다.
DETR은 Faster R-CNN과 비슷한 성능을 보이면서도 heuristic한 과정이나 post-processing을 필요하지 않는다는 점에서 매우 큰 장점을 가집니다. 하지만 DETR의 경우 모델의 학습 수렴 속도가 매우 느리며, 작은 객체에 대한 성능이 기존의 모델들보다 떨어집니다. 이를 개선한 논문들도 후에 리뷰하도록 하겠습니다.
참고
[1] https://arxiv.org/pdf/2005.12872
[2] https://herbwood.tistory.com/26
[3] https://kimjy99.github.io/%EB%85%BC%EB%AC%B8%EB%A6%AC%EB%B7%B0/detr/
'Paper Review' 카테고리의 다른 글
| [YOLO v3] An Imcremental Improvement (0) | 2024.07.24 |
|---|---|
| [YOLO v2] YOLO9000: Better, Faster, Stronger (0) | 2024.07.19 |
| [SSD] Single Shot MultiBox Detector (0) | 2024.07.16 |
| [YOLO v1] You Only Look Once: Unified, Real-Time Object Detection (0) | 2024.07.15 |
| [ViT] Vision Transformer, AN IMAGE IS WORTH 16X16 WORDS:TRANSFORMERS FOR IMAGE RECOGNITION AT SCALE (0) | 2024.07.12 |
