Gradient Descent
경사 하강법(Gradient Descent)은 함수의 기울기(Gradient)를 이용하여 비용 함수(Cost Function)의 최소값을 찾는 최적화(Optimize) 알고리즘입니다.
먼저, 함수의 최소값을 찾기 위해서는 미분을 통해 함수의 기울기를 구해야 합니다.
경사 하강법은 초기에 임의의 가중치(Weight)를 가지고 시작합니다.
이후 각 가중치에 대한 함수의 기울기(Gradient)를 계산하여 기울기가 작아지는 방향으로 가중치를 업데이트 합니다.
여기서 기울기가 작아지는 방향이란 함수의 기울기가 0인 지점(최소값)으로 가능 방향입니다. 이를 식으로 나타내면 다음과 같습니다.
$$ w = w - \eta \frac{\partial loss}{\partial w} $$
여기서 w는 업데이트할 가중치, \(\eta\)는 학습률(learning rate)이며, \(\frac{\partial loss}{\partial w}\)는 가중치에 대한 함수의 기울기 입니다.
여기서 loss는 함수가 예측한 값과 실제 값 사이의 오차를 계산한 값입니다. 즉 Gradient Descent는 이 loss의 값을 줄이기 위해 w를 업데이트하는 과정의 반복입니다.

위 그림에서 대칭축을 기준으로 오른쪽 영역에 있는 한 지점에서 미분값을 구하면 기울기는 양수일 것입니다.
learning rate도 양수, 기울기도 양수이기 때문에 갱신 시 w는 감소하여 최솟값 지점으로 이동하게 됩니다.
마찬가지로 대칭축을 기준으로 왼쪽 영역에 있는 한 지점에서 미분값을 구하면 음수일 것입니다.
learning rate가 양수, 기울기가 음수이면 갱신시 w는 증가하여 최소값 지점으로 이동하게 됩니다.
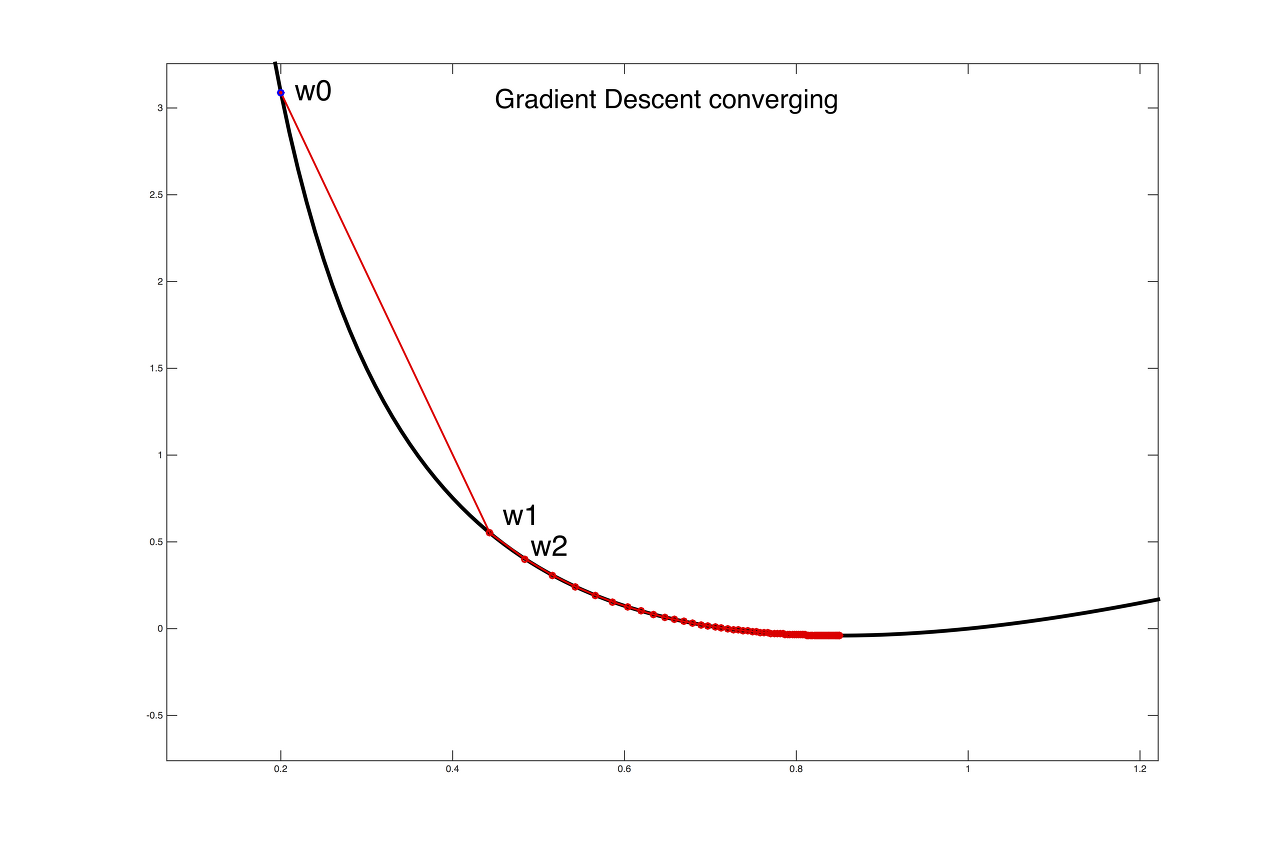

이 과정을 반복하면서 함수의 최소값으로 수렴하게 됩니다. 학습률은 가중치를 업데이트 하는 양을 조절하는 역할을 하며, 적절한 학습률을 선택해야 수렴 속도가 빨라지면서도 안정적으로 최소값에 도달할 수 있습니다. 만약 학습률을 너무 적거나 너무 크게 설정하면 수렴이 하는데 많은 시간이 걸리게 되거나 학습이 진행되지 않을 수 있습니다.
문제점
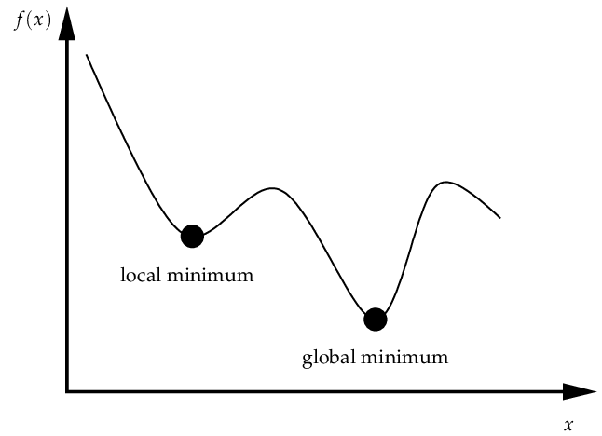
하지만 위 그림처럼 경사 하강법은 전체 영역에서 최소값(Global minimum)이 아닌 지역에서 최소값(Local minimum)에 수렴할 가능성이 있으며, 이는 함수가 복잡하고 비선형적일 때 더욱 빈번하게 발생합니다. 또한 gradient가 0에 가까워지는 지점에서는 학습 속도가 현저히 느려지거나 멈추는 경향이 있어 수렴이 어려워집니다.
또한, 경사 하강법은 모든 훈련 데이터에 대해 파라미터를 업데이트해야 합니다. 따라서 훈련 데이터가 매우 클 경우, 계산 비용이 매우 커질 수 있으며, 초기 파라미터 값에 매우 민감하여 초기 값에 따라 학습이 잘 되지 않을 수 있습니다.
Stochastic Gradient Descent (SGD)
SGD도 Gradient Descent와 마찬가지로 모델이 예측한 값과 실제 값 사이의 오차(loss)를 계산한 후, 해당 오차를 최소화 하기 위해 가중치를 업데이트하는 것입니다. 이 때, Gradient Descent 처럼 모든 데이터에 대한 오차를 계산하고 가중치를 업데이트하는 것이 아니라, 랜덤하게(확률적으로) 선택(샘플링)된 일부 데이터(미니 배치)에 대해서만 오차를 계산하고 가중치를 업데이트 합니다.
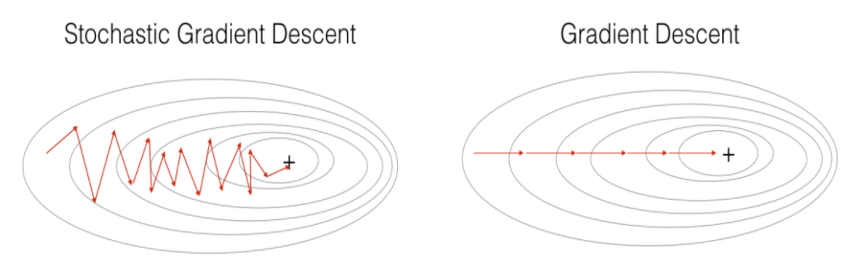
계산 속도가 훨씬 빠르기 때문에 같은 시간에 더 많은 step을 갈 수 있으며, Local Minima에 빠지지 않고 더 좋은 방향으로 수렴할 가능성이 높다.
아래 그림에서 SGD는 입력 데이터를 한 개만 사용했을 때의 그림이고,
Mini-Batch Gradient Descent는 입력 데이터를 미니 배치로 묶어 사용했을 때의 그림이다.

Momentum
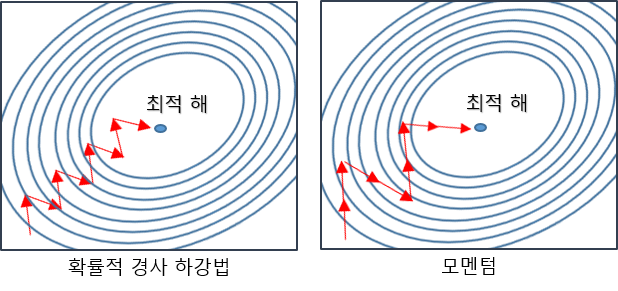
Momentum은 SGD의 편차를 줄이고 수렴을 부드럽게 하기 위해 고안되었습니다.
Momentum은 현재 위치에서 기울기와 함께 이전 단계에서의 이동 방향과 크기를 고려하여 이동합니다.
이를 위해 Moment 라는 값을 사용하는데, Moment(\(\alpha\))는 현재 위치에서의 기울기와 이전 단계에서의 Moment(\(\alpha\)) 값을 일정 비율로 결합한 것입니다. 따라서, 이전에 이동한 방향과 크기가 현재 위치에서의 이동 방향과 크기를 결정하는 데 영향을 미치게 되며, Local Minima에서 탈출 할 수 있는 효과가 있습니다.
다음 수식에서 v는 물리에서 말하는 속도(velocity) 입니다.
$$ V(t) = \alpha V(t-1) - \eta \frac{\partial}{\partial w} Cost(w) $$
$$ w(t+1) = w(t) + V(t) $$
class Momentum:
def __init__(self, lr = 0.01, momentum = 0.9):
self.lr = lr
self.momentum = momentum
self.v = None
def update(self, params, grads):
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_list(val)
for key in params.keys():
self.v[key] = self.momentum * self.v[key] - self.lr * self.grads[key]
self.params[key] += self.v[key]
Adagrad
Adagrad는 일반적으로 학습률을 일정하게 유지하며 모든 매개 변수에 대해 같은 학습률을 적용하는 SGD나 Momentum과 달리 각 파라미터마다 서로 다른 학습률을 적용합니다.
Adagrad는 과거의 기울기 값을 저장해두었다가 이를 사용하여 학습률을 조정합니다. 조정하는 방법은 많이 변화하지 않은 변수들은 학습률을 크게하고 반대로 많이 변화한 변수들에 대해서는 학습률을 적게 하는 방법입니다. 각 파라미터마다 각각의 학습률을 사용하므로, 전체 파라미터의 학습률을 조절하는 것보다 더욱 미세한 조정이 가능합니다.
$$ G(t) = G(t-1) + (\frac{\partial}{\partial w(t)} Cost(w(t))^2 = \sum_{i=0}^t (\frac{\partial}{\partial w(i)} Cost(w(i)))^2 $$
$$ w(t+1) = w(t) - \eta \frac{1}{\sqrt{G(t)+\epsilon}} \frac{\partial}{\partial w(i)} Cost(w(i))$$
이 수식에서 \(G(t)\)는 t번째 time까지의 기울기 누적 크기이며 \(\epsilon\)과 더해진 후 루트가 적용되고 \(\eta\)(학습률)에 나누어 집니다. \(\epsilon\)은 매우 작은 상수 값으로, 0으로 나누어지는 것을 방지해 줍니다. 이 부분이 매개변수의 원소 중에서 많이 변화한 변수에 대해서는 학습률을 적게 갱신하고, 적게 변화한 변수에 대해서는 크게 갱신해주는 부분입니다.
class AdaGrad:
def __init__(self, lr = 0.01):
self.lr = lr
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] += grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
RMSprop
Adagrad의 문제점은 과거의 모든 기울기 값을 누적하기 때문에 학습을 진행하면 할수록 \(G(t)\)의 값이 커지므로 학습률이 너무 작아져 결국 학습이 멈출 수 있습니다.
RMSprop은 이러한 문제를 해결하기 위해, 지수 이동 평균(Expoential Moving Average)을 사용합니다. 이는 과거의 값이 더 적게 반영되도록 하는 가중치를 사용하여 현재 값과 과거 값의 평균을 계산하는 방법입니다.
지수 이동 평균은 시계열 데이터에서 최근 데이터를 더 강조하기 위해, 지수 함수를 사용하여 가중치를 부여해 평균을 계산하는 방법입니다.
$$ x_t = \alpha p_t + (1-\alpha) x_{t-1}, where \alpha=\frac{2}{N+1} $$
여기에서 지수 이동 평균 값은 \(x\), 현재 값은 \(p\), 가중치는 \(\alpha\)이며, \(t\)는 step 또는 시간, \(N\)은 값의 개수 입니다. \((1-\alpha)\)가 매 step마다 곱해지는데 이는 1보다 작기 때문에 시간이 지날수록 영향력이 줄어드는 것을 확인할 수 있습니다.
RMSprop의 수식은 다음과 같습니다.
$$ G(t) = \gamma G(t-1) + (1-\gamma)(\frac{\partial}{\partial w(i)} Cost(w(i)))^2 $$
$$ w(t+1) = w(t) - \eta \frac{1}{\sqrt{G(t)+\epsilon}} \frac{\partial}{\partial w(i)} Cost(w(i)) $$
Adagrad에서는 \(G(t)\)가 그냥 더해지지만, RMSprop에서는 \(G(t)\)에서 지수 이동 평균이 사용됩니다.
class AdaGrad:
def __init__(self, lr = 0.01):
self.lr = lr
self.h = None
self.gamma = 0.9
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] = self.gamma * self.h[key] + (1-self.gamma) * grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
Adam
Adam은 RMSprop와 Momentum을 합친 방법입니다.
수식을 보면 더욱 쉽게 이해할 수 있습니다.
$$ M(t) = \beta_1 M(t-1) + (1-\beta_1) \frac{\partial}{\partial w(t)} Cost(w(t)) $$
$$ V(t) = \beta_2 V(t-1) + (1-\beta_2) (\frac{\partial}{\partial w(i)} Cost(w(i)))^2 $$
$$ \hat{M(t)} = \frac{M(t)}{1-\beta_1^t} , \hat{V(t)} = \frac{V(t)}{1-\beta_2^t} $$
$$ w(t+1) = w(t) - \eta \frac{\hat{M(t)}}{\sqrt{\hat{V(t)} + \epsilon}} $$
\(M(t)\)는 그레디언트의 지수 이동 평균을, \(V(t)\)는 그레디언트 제곱의 지수 이동 평균을 구합니다.
\(\hat{M(t)}\)와 \(\hat{V(t)}\)는 논문에서 bias(편향)가 수정된 값으로 변경하는 과정이라고 하였습니다.
이는 Adam의 초기 학습 단계에서 그레디언트가 작을 때, 적절한 학습률을 선택하기 위해 bias 보정을 수행합니다.
'ML & DL > 기초 이론' 카테고리의 다른 글
| Probability Model(확률 모형), Random Variable(확률 변수) (0) | 2023.03.22 |
|---|---|
| Regularization: Overfitting을 해결하는 방법들 (0) | 2023.03.21 |
| Overfitting & Underfitting (0) | 2023.03.21 |
| Neural Network & Linear Neural Networks & Multi Layer Perceptron (0) | 2023.03.20 |
| [CNN] Convolution Neural Network 정리 (0) | 2022.01.27 |
Gradient Descent
경사 하강법(Gradient Descent)은 함수의 기울기(Gradient)를 이용하여 비용 함수(Cost Function)의 최소값을 찾는 최적화(Optimize) 알고리즘입니다.
먼저, 함수의 최소값을 찾기 위해서는 미분을 통해 함수의 기울기를 구해야 합니다.
경사 하강법은 초기에 임의의 가중치(Weight)를 가지고 시작합니다.
이후 각 가중치에 대한 함수의 기울기(Gradient)를 계산하여 기울기가 작아지는 방향으로 가중치를 업데이트 합니다.
여기서 기울기가 작아지는 방향이란 함수의 기울기가 0인 지점(최소값)으로 가능 방향입니다. 이를 식으로 나타내면 다음과 같습니다.
$$ w = w - \eta \frac{\partial loss}{\partial w} $$
여기서 w는 업데이트할 가중치, \(\eta\)는 학습률(learning rate)이며, \(\frac{\partial loss}{\partial w}\)는 가중치에 대한 함수의 기울기 입니다.
여기서 loss는 함수가 예측한 값과 실제 값 사이의 오차를 계산한 값입니다. 즉 Gradient Descent는 이 loss의 값을 줄이기 위해 w를 업데이트하는 과정의 반복입니다.

위 그림에서 대칭축을 기준으로 오른쪽 영역에 있는 한 지점에서 미분값을 구하면 기울기는 양수일 것입니다.
learning rate도 양수, 기울기도 양수이기 때문에 갱신 시 w는 감소하여 최솟값 지점으로 이동하게 됩니다.
마찬가지로 대칭축을 기준으로 왼쪽 영역에 있는 한 지점에서 미분값을 구하면 음수일 것입니다.
learning rate가 양수, 기울기가 음수이면 갱신시 w는 증가하여 최소값 지점으로 이동하게 됩니다.


이 과정을 반복하면서 함수의 최소값으로 수렴하게 됩니다. 학습률은 가중치를 업데이트 하는 양을 조절하는 역할을 하며, 적절한 학습률을 선택해야 수렴 속도가 빨라지면서도 안정적으로 최소값에 도달할 수 있습니다. 만약 학습률을 너무 적거나 너무 크게 설정하면 수렴이 하는데 많은 시간이 걸리게 되거나 학습이 진행되지 않을 수 있습니다.
문제점

하지만 위 그림처럼 경사 하강법은 전체 영역에서 최소값(Global minimum)이 아닌 지역에서 최소값(Local minimum)에 수렴할 가능성이 있으며, 이는 함수가 복잡하고 비선형적일 때 더욱 빈번하게 발생합니다. 또한 gradient가 0에 가까워지는 지점에서는 학습 속도가 현저히 느려지거나 멈추는 경향이 있어 수렴이 어려워집니다.
또한, 경사 하강법은 모든 훈련 데이터에 대해 파라미터를 업데이트해야 합니다. 따라서 훈련 데이터가 매우 클 경우, 계산 비용이 매우 커질 수 있으며, 초기 파라미터 값에 매우 민감하여 초기 값에 따라 학습이 잘 되지 않을 수 있습니다.
Stochastic Gradient Descent (SGD)
SGD도 Gradient Descent와 마찬가지로 모델이 예측한 값과 실제 값 사이의 오차(loss)를 계산한 후, 해당 오차를 최소화 하기 위해 가중치를 업데이트하는 것입니다. 이 때, Gradient Descent 처럼 모든 데이터에 대한 오차를 계산하고 가중치를 업데이트하는 것이 아니라, 랜덤하게(확률적으로) 선택(샘플링)된 일부 데이터(미니 배치)에 대해서만 오차를 계산하고 가중치를 업데이트 합니다.
계산 속도가 훨씬 빠르기 때문에 같은 시간에 더 많은 step을 갈 수 있으며, Local Minima에 빠지지 않고 더 좋은 방향으로 수렴할 가능성이 높다.
아래 그림에서 SGD는 입력 데이터를 한 개만 사용했을 때의 그림이고,
Mini-Batch Gradient Descent는 입력 데이터를 미니 배치로 묶어 사용했을 때의 그림이다.


Momentum

Momentum은 SGD의 편차를 줄이고 수렴을 부드럽게 하기 위해 고안되었습니다.
Momentum은 현재 위치에서 기울기와 함께 이전 단계에서의 이동 방향과 크기를 고려하여 이동합니다.
이를 위해 Moment 라는 값을 사용하는데, Moment(\(\alpha\))는 현재 위치에서의 기울기와 이전 단계에서의 Moment(\(\alpha\)) 값을 일정 비율로 결합한 것입니다. 따라서, 이전에 이동한 방향과 크기가 현재 위치에서의 이동 방향과 크기를 결정하는 데 영향을 미치게 되며, Local Minima에서 탈출 할 수 있는 효과가 있습니다.
다음 수식에서 v는 물리에서 말하는 속도(velocity) 입니다.
$$ V(t) = \alpha V(t-1) - \eta \frac{\partial}{\partial w} Cost(w) $$
$$ w(t+1) = w(t) + V(t) $$
class Momentum:
def __init__(self, lr = 0.01, momentum = 0.9):
self.lr = lr
self.momentum = momentum
self.v = None
def update(self, params, grads):
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_list(val)
for key in params.keys():
self.v[key] = self.momentum * self.v[key] - self.lr * self.grads[key]
self.params[key] += self.v[key]
Adagrad
Adagrad는 일반적으로 학습률을 일정하게 유지하며 모든 매개 변수에 대해 같은 학습률을 적용하는 SGD나 Momentum과 달리 각 파라미터마다 서로 다른 학습률을 적용합니다.
Adagrad는 과거의 기울기 값을 저장해두었다가 이를 사용하여 학습률을 조정합니다. 조정하는 방법은 많이 변화하지 않은 변수들은 학습률을 크게하고 반대로 많이 변화한 변수들에 대해서는 학습률을 적게 하는 방법입니다. 각 파라미터마다 각각의 학습률을 사용하므로, 전체 파라미터의 학습률을 조절하는 것보다 더욱 미세한 조정이 가능합니다.
$$ G(t) = G(t-1) + (\frac{\partial}{\partial w(t)} Cost(w(t))^2 = \sum_{i=0}^t (\frac{\partial}{\partial w(i)} Cost(w(i)))^2 $$
$$ w(t+1) = w(t) - \eta \frac{1}{\sqrt{G(t)+\epsilon}} \frac{\partial}{\partial w(i)} Cost(w(i))$$
이 수식에서 \(G(t)\)는 t번째 time까지의 기울기 누적 크기이며 \(\epsilon\)과 더해진 후 루트가 적용되고 \(\eta\)(학습률)에 나누어 집니다. \(\epsilon\)은 매우 작은 상수 값으로, 0으로 나누어지는 것을 방지해 줍니다. 이 부분이 매개변수의 원소 중에서 많이 변화한 변수에 대해서는 학습률을 적게 갱신하고, 적게 변화한 변수에 대해서는 크게 갱신해주는 부분입니다.
class AdaGrad:
def __init__(self, lr = 0.01):
self.lr = lr
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] += grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
RMSprop
Adagrad의 문제점은 과거의 모든 기울기 값을 누적하기 때문에 학습을 진행하면 할수록 \(G(t)\)의 값이 커지므로 학습률이 너무 작아져 결국 학습이 멈출 수 있습니다.
RMSprop은 이러한 문제를 해결하기 위해, 지수 이동 평균(Expoential Moving Average)을 사용합니다. 이는 과거의 값이 더 적게 반영되도록 하는 가중치를 사용하여 현재 값과 과거 값의 평균을 계산하는 방법입니다.
지수 이동 평균은 시계열 데이터에서 최근 데이터를 더 강조하기 위해, 지수 함수를 사용하여 가중치를 부여해 평균을 계산하는 방법입니다.
$$ x_t = \alpha p_t + (1-\alpha) x_{t-1}, where \alpha=\frac{2}{N+1} $$
여기에서 지수 이동 평균 값은 \(x\), 현재 값은 \(p\), 가중치는 \(\alpha\)이며, \(t\)는 step 또는 시간, \(N\)은 값의 개수 입니다. \((1-\alpha)\)가 매 step마다 곱해지는데 이는 1보다 작기 때문에 시간이 지날수록 영향력이 줄어드는 것을 확인할 수 있습니다.
RMSprop의 수식은 다음과 같습니다.
$$ G(t) = \gamma G(t-1) + (1-\gamma)(\frac{\partial}{\partial w(i)} Cost(w(i)))^2 $$
$$ w(t+1) = w(t) - \eta \frac{1}{\sqrt{G(t)+\epsilon}} \frac{\partial}{\partial w(i)} Cost(w(i)) $$
Adagrad에서는 \(G(t)\)가 그냥 더해지지만, RMSprop에서는 \(G(t)\)에서 지수 이동 평균이 사용됩니다.
class AdaGrad:
def __init__(self, lr = 0.01):
self.lr = lr
self.h = None
self.gamma = 0.9
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] = self.gamma * self.h[key] + (1-self.gamma) * grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
Adam
Adam은 RMSprop와 Momentum을 합친 방법입니다.
수식을 보면 더욱 쉽게 이해할 수 있습니다.
$$ M(t) = \beta_1 M(t-1) + (1-\beta_1) \frac{\partial}{\partial w(t)} Cost(w(t)) $$
$$ V(t) = \beta_2 V(t-1) + (1-\beta_2) (\frac{\partial}{\partial w(i)} Cost(w(i)))^2 $$
$$ \hat{M(t)} = \frac{M(t)}{1-\beta_1^t} , \hat{V(t)} = \frac{V(t)}{1-\beta_2^t} $$
$$ w(t+1) = w(t) - \eta \frac{\hat{M(t)}}{\sqrt{\hat{V(t)} + \epsilon}} $$
\(M(t)\)는 그레디언트의 지수 이동 평균을, \(V(t)\)는 그레디언트 제곱의 지수 이동 평균을 구합니다.
\(\hat{M(t)}\)와 \(\hat{V(t)}\)는 논문에서 bias(편향)가 수정된 값으로 변경하는 과정이라고 하였습니다.
이는 Adam의 초기 학습 단계에서 그레디언트가 작을 때, 적절한 학습률을 선택하기 위해 bias 보정을 수행합니다.
'ML & DL > 기초 이론' 카테고리의 다른 글
| Probability Model(확률 모형), Random Variable(확률 변수) (0) | 2023.03.22 |
|---|---|
| Regularization: Overfitting을 해결하는 방법들 (0) | 2023.03.21 |
| Overfitting & Underfitting (0) | 2023.03.21 |
| Neural Network & Linear Neural Networks & Multi Layer Perceptron (0) | 2023.03.20 |
| [CNN] Convolution Neural Network 정리 (0) | 2022.01.27 |
