Probability Model, 확률 모형
확률 모형은 어떤 사건이 발생할 가능성(확률)을 수학적으로 만든 방법입니다.
이는 확률 변수(random variable)라는 것을 이용하여 데이터 분포를 수학적으로 정의하는 방법라고도 합니다.
보통 미리 정해진 확률 분포 함수 또는 확률 밀도 함수를 사용하며, 이 함수들의 계수를 모수(parameter)라고 부릅니다.
모수(parameter)는 \(\theta\)라고 표기하기도 하며, 이는 확률 모형을 정의하는 데 중요한 역할을 하는 값으로 요약 통계량(Descriptive Measure)라고 부릅니다.
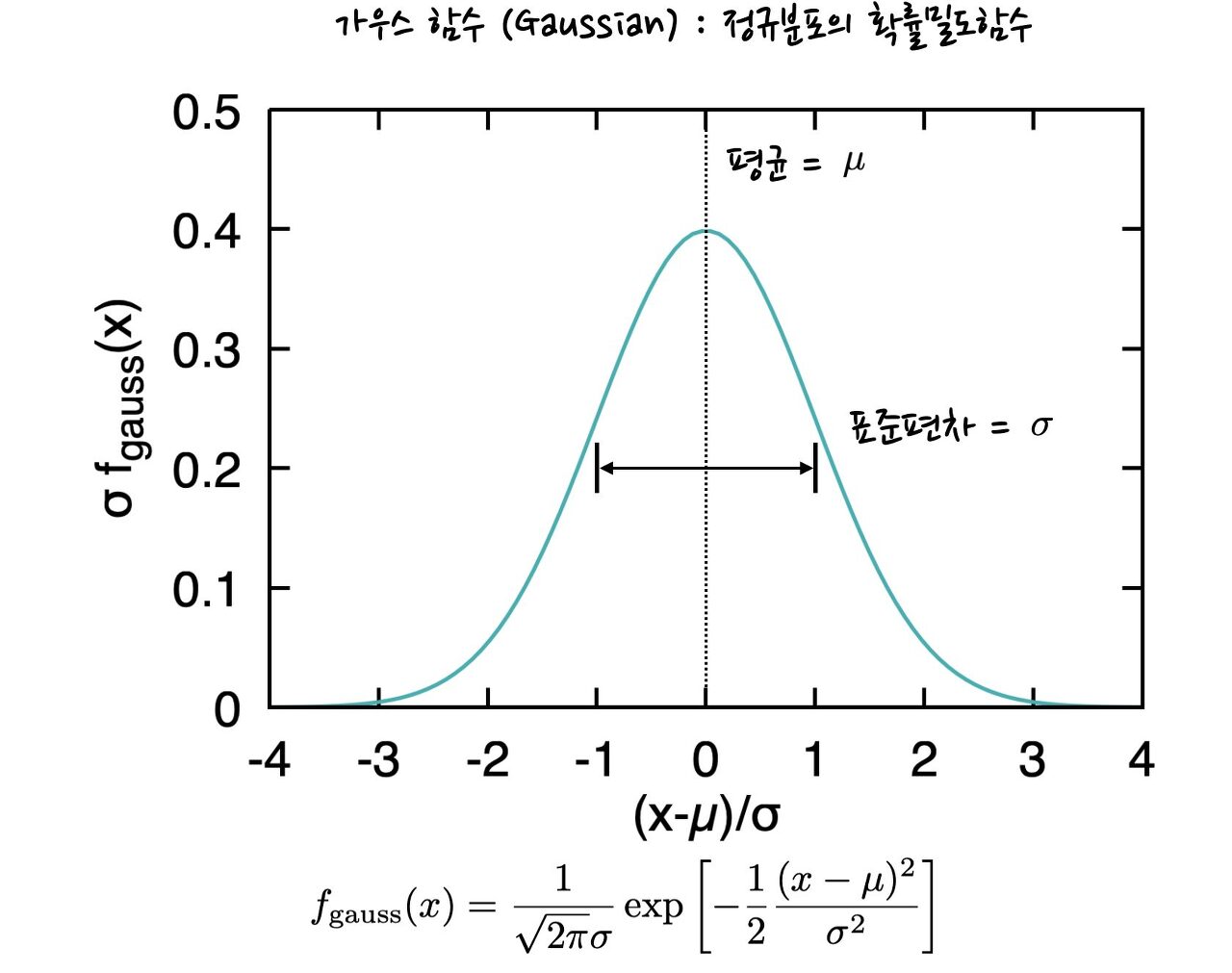
예를 들어 가장 널리 쓰이는 확률 모형의 하나인 가우시안 정규 분포(Gaussian normal distribution)는 다음과 같은 수식으로 확률 밀도 함수를 정의한다.
$$ N(x; \mu, \sigma) = \frac{1}{\sigma\sqrt{2\pi}}\, e^{-\frac{(x - \mu)^2}{2 \sigma^2}} $$
이 함수의 독립 변수는 자료의 값을 의미하는 변수 \(x\)이다. 이 식에서 사용된 \(\mu\)와 \(\sigma\)는 평균(mean)과 표준편차(standard deviation)를 뜻하는 모수이다.
가우시안 정규 분포가 범용성을 가질 수 있는 이유 중 하나는 평균과 표준편차를 알면 그형태를 완벽하게 특정할 수 있다는 점이다. 뿐만 아니라 변수를 세번 이상 거듭제곱한 뒤에 그 평균을 구해도 유한한 값으로 수렴한다는 것 역시 계산을 편리하게 해 주는 요소이다.
확률 변수 (Random Variable)
확률 변수는 어떤 확률 분포와 연관된 변수를 말합니다.
어떤 자료의 값이 분포가 특정한 확률 모형과 일치하는 경우 그 자료를 확률 변수라고 하고 해당 확률 모형을 따른다고 말합니다.
확률 변수는 보통 \(X\), \(Y\) 같이 알파벳 대문자로 표시하며 확률 변수 \(X\)가 정규 분포를 따른 경우 수학적으로 다음과 같이 표기합니다.
$$ X \sim N(\mu, \sigma) $$
확률 변수와 확률 모형의 아주 간단한 예시로, \(X\)가 \(Bernoulli(p)\)를 따른다면 X는 0 또는 1이 나올 수 있습니다. 여기서 Bernoulli가 확률 모형, X가 확률 변수라고 할 수 있습니다.
확률 변수는 보통 이산형(discrete)과 연속형(continuous)로 분류됩니다.
이산형 확률 변수는 유한 개 또는 셀 수 있는(infinite countable) 값 즉, 정수인 경우를 의미합니다.
이산형 확률 변수를 가진 함수를 확률 질량 함수라고 합니다.
반대로, 연속 확률 변수는 연속적인 값 즉, 실수인 경우를 의미합니다.
연속 확률 변수를 가진 함수를 확률 밀도 함수라고 합니다.
'ML & DL > 기초 이론' 카테고리의 다른 글
| Transfer Learning & Knowledge distillation (0) | 2023.03.31 |
|---|---|
| Parameter Estimation (모수 추정), 가능도 (Likelihood), MLE (Maximum Likelihood Estimation) (0) | 2023.03.22 |
| Regularization: Overfitting을 해결하는 방법들 (0) | 2023.03.21 |
| Overfitting & Underfitting (0) | 2023.03.21 |
| Gradient Descent & Optimizer(SGD, Momentum, Adagrad, RMSprop, Adam) (0) | 2023.03.20 |
Probability Model, 확률 모형
확률 모형은 어떤 사건이 발생할 가능성(확률)을 수학적으로 만든 방법입니다.
이는 확률 변수(random variable)라는 것을 이용하여 데이터 분포를 수학적으로 정의하는 방법라고도 합니다.
보통 미리 정해진 확률 분포 함수 또는 확률 밀도 함수를 사용하며, 이 함수들의 계수를 모수(parameter)라고 부릅니다.
모수(parameter)는 \(\theta\)라고 표기하기도 하며, 이는 확률 모형을 정의하는 데 중요한 역할을 하는 값으로 요약 통계량(Descriptive Measure)라고 부릅니다.
예를 들어 가장 널리 쓰이는 확률 모형의 하나인 가우시안 정규 분포(Gaussian normal distribution)는 다음과 같은 수식으로 확률 밀도 함수를 정의한다.
$$ N(x; \mu, \sigma) = \frac{1}{\sigma\sqrt{2\pi}}\, e^{-\frac{(x - \mu)^2}{2 \sigma^2}} $$
이 함수의 독립 변수는 자료의 값을 의미하는 변수 \(x\)이다. 이 식에서 사용된 \(\mu\)와 \(\sigma\)는 평균(mean)과 표준편차(standard deviation)를 뜻하는 모수이다.
가우시안 정규 분포가 범용성을 가질 수 있는 이유 중 하나는 평균과 표준편차를 알면 그형태를 완벽하게 특정할 수 있다는 점이다. 뿐만 아니라 변수를 세번 이상 거듭제곱한 뒤에 그 평균을 구해도 유한한 값으로 수렴한다는 것 역시 계산을 편리하게 해 주는 요소이다.

확률 변수 (Random Variable)
확률 변수는 어떤 확률 분포와 연관된 변수를 말합니다.
어떤 자료의 값이 분포가 특정한 확률 모형과 일치하는 경우 그 자료를 확률 변수라고 하고 해당 확률 모형을 따른다고 말합니다.
확률 변수는 보통 \(X\), \(Y\) 같이 알파벳 대문자로 표시하며 확률 변수 \(X\)가 정규 분포를 따른 경우 수학적으로 다음과 같이 표기합니다.
$$ X \sim N(\mu, \sigma) $$
확률 변수와 확률 모형의 아주 간단한 예시로, \(X\)가 \(Bernoulli(p)\)를 따른다면 X는 0 또는 1이 나올 수 있습니다. 여기서 Bernoulli가 확률 모형, X가 확률 변수라고 할 수 있습니다.
확률 변수는 보통 이산형(discrete)과 연속형(continuous)로 분류됩니다.
이산형 확률 변수는 유한 개 또는 셀 수 있는(infinite countable) 값 즉, 정수인 경우를 의미합니다.
이산형 확률 변수를 가진 함수를 확률 질량 함수라고 합니다.
반대로, 연속 확률 변수는 연속적인 값 즉, 실수인 경우를 의미합니다.
연속 확률 변수를 가진 함수를 확률 밀도 함수라고 합니다.
'ML & DL > 기초 이론' 카테고리의 다른 글
| Transfer Learning & Knowledge distillation (0) | 2023.03.31 |
|---|---|
| Parameter Estimation (모수 추정), 가능도 (Likelihood), MLE (Maximum Likelihood Estimation) (0) | 2023.03.22 |
| Regularization: Overfitting을 해결하는 방법들 (0) | 2023.03.21 |
| Overfitting & Underfitting (0) | 2023.03.21 |
| Gradient Descent & Optimizer(SGD, Momentum, Adagrad, RMSprop, Adam) (0) | 2023.03.20 |
